【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图

根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.
参考答案:
【答案】(1)450、63; ⑵36°,图见解析; (3)2460 人.
【解析】
(1)根据“骑电动车”上下的人数除以所占的百分比,即可得到调查学生数;用调查学生数乘以选择![]() 类的人数所占的百分比,即可求出选择
类的人数所占的百分比,即可求出选择![]() 类的人数.
类的人数.
(2)求出![]() 类的百分比,乘以
类的百分比,乘以![]() 即可求出
即可求出![]() 类对应的扇形圆心角
类对应的扇形圆心角![]() 的度数;由总学生数求出选择公共交通的人数,补全统计图即可;
的度数;由总学生数求出选择公共交通的人数,补全统计图即可;
(3)由总人数乘以“绿色出行”的百分比,即可得到结果.
(1) 参与本次问卷调查的学生共有:![]() (人);
(人);
选择![]() 类的人数有:
类的人数有:![]()
故答案为:450、63;
(2)![]() 类所占的百分比为:
类所占的百分比为:![]()
![]() 类对应的扇形圆心角
类对应的扇形圆心角![]() 的度数为:
的度数为:![]()
选择![]() 类的人数为:
类的人数为:![]() (人).
(人).
补全条形统计图为:
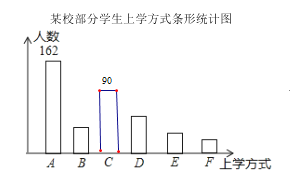
(3) 估计该校每天“绿色出行”的学生人数为3000×(1-14%-4%)=2460 人.
-
科目: 来源: 题型:
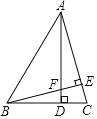
查看答案和解析>>【题目】如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中, ,点
,点 在边
在边 上,且
上,且 .将
.将 沿
沿 对折至
对折至 ,延长
,延长 交边
交边 于点
于点 .连结
.连结 、
、 .下列结论:①
.下列结论:① ;②
;② ;③
;③ 是正三角形;④
是正三角形;④ 的面积为90.其中正确的是______(填所有正确答案的序号).
的面积为90.其中正确的是______(填所有正确答案的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.
理解:(1)如图
 ,已知
,已知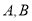 是⊙
是⊙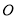 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点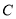 ,使
,使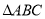 为“智慧三角形”(画出点
为“智慧三角形”(画出点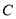 的位置,保留作图痕迹);
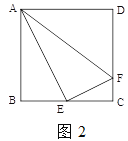
的位置,保留作图痕迹);(2)如图
 ,在正方形
,在正方形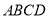 中,
中, 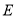 是
是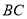 的中点,
的中点, 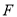 是
是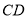 上一点,且
上一点,且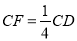 ,试判断
,试判断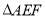 是否为“智慧三角形”,并说明理由;
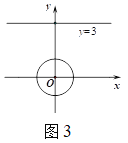
是否为“智慧三角形”,并说明理由;运用:(3)如图
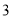 ,在平面直角坐标系
,在平面直角坐标系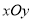 中,⊙
中,⊙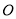 的半径为
的半径为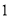 ,点
,点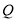 是直线
是直线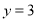 上的一点,若在⊙
上的一点,若在⊙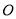 上存在一点
上存在一点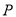 ,使得
,使得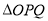 为“智慧三角形”,其面积的最小值为______.
为“智慧三角形”,其面积的最小值为______.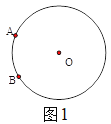
-
科目: 来源: 题型:
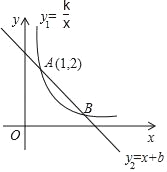
查看答案和解析>>【题目】反比例函数y1=
 (x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)(1)求这两个函数解析式;
(2)在y轴上求作一点P,使PA+PB的值最小,并直接写出此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有
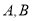 两种型号的健身器可供选择.
两种型号的健身器可供选择.(1)劲松公司2015年每套
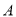 型健身器的售价为
型健身器的售价为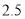 万元,经过连续两年降价,2017年每套售价为
万元,经过连续两年降价,2017年每套售价为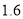 万元,求每套
万元,求每套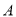 型健身器年平均下降率
型健身器年平均下降率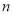 ;
;(2)2017年市政府经过招标,决定年内采购并安装劲松公司
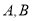 两种型号的健身器材共
两种型号的健身器材共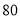 套,采购专项费总计不超过
套,采购专项费总计不超过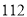 万元,采购合同规定:每套
万元,采购合同规定:每套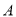 型健身器售价为
型健身器售价为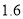 万元,每套
万元,每套 型健身器售价我
型健身器售价我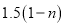 万元.
万元.①
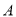 型健身器最多可购买多少套?
型健身器最多可购买多少套? ②安装完成后,若每套
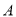 型和
型和 型健身器一年的养护费分别是购买价的
型健身器一年的养护费分别是购买价的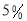 和
和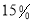 .市政府计划支出
.市政府计划支出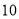 万元进行养护.问该计划支出能否满足一年的养护需要?
万元进行养护.问该计划支出能否满足一年的养护需要? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,(1)求m,n,b的值;
(2)求tan∠ACB;
(3)探究在点D运动过程中,是否存在∠DEA=45°,若存在,则求此时线段AE的长;若不存在,请说明理由.

相关试题

