【题目】在崇仁一中中学生篮球赛中,小方共打了10场球.他在第6,7,8,9场比赛中分别得了22,15,12和19分,他的前9场比赛的平均得分y比前5场比赛的平均得分x要高 .如果他所参加的10场比赛的平均得分超过18分
(1)用含x的代数式表示y;
(2)小方在前5场比赛中,总分可达到的最大值是多少?
(3)小方在第10场比赛中,得分可达到的最小值是多少?
参考答案:
【答案】(1)![]() ;
;
(2)小方在前5场比赛中总分的最大值应为84分;
(3)小方在第10场比赛中得分的最小值应为29分 .
【解析】
试题(1)由题意不难看出,前五场的总得分为5x,前9场总得分为9y,所以9y=5x+22+15+12+19,即![]() ;
;
(2)因为9场比赛的平均得分y比前5场比赛的平均得分x要高,即y>x.所以有y=![]()
>x,解不等式即可求出x的最大值,进而求出前5场最高得分;
(3)因为10场比赛的平均得分超过18分,所以10场比赛的总得分超过180分.也就是说前5场的最高分加上6、7、8、9四场的总得分再加上第10场得分大于180分,从而确定出第10场的最低分.(篮球比赛中的得分都是整数,不存在0.5分)
试题解析:(1)![]() ;
;
(2)由题意有![]() ,解得x<17,
,解得x<17,
所以小方在前5场比赛中总分的最大值应为17×5-1=84分;
(3)又由题意,小方在这10场比赛中得分至少为18×10 + 1=181分,
设他在第10场比赛中的得分为S,则有84+(22+15+12+19)+ S ≥181 .
解得S≥29,所以小方在第10场比赛中得分的最小值应为29分 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是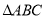 的外接圆,
的外接圆,  点在
点在 边上,
边上, 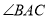 的平分线交
的平分线交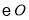 于点
于点 ,连接
,连接 ,过点
,过点 作
作 的平行线,与
的平行线,与 的延长线相交于点
的延长线相交于点 .
.(1)求证:
 是
是 的切线;
的切线;(2)求证:△PBD∽△DCA;
(3)当
 时,求线段
时,求线段 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.
计时制:0.05元/分;
包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1)求证:CA=CN;
(2)连接DF,若cos∠DFA=
 ,AN=
,AN= ,求圆O的直径的长度.
,求圆O的直径的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.

(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 与
与 轴交于
轴交于 ,
,  ,与
,与 轴交于
轴交于 .
. (1)若
 ,求抛物线的解析式,并写出抛物线的对称轴;
,求抛物线的解析式,并写出抛物线的对称轴;(2)如图1,在(1)的条件下,设抛物线的对称轴交轴于
 ,在对称轴左侧的抛物线上有一点
,在对称轴左侧的抛物线上有一点 ,使
,使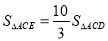 ,求点
,求点 的坐标;
的坐标;(3)如图2,设
 ,
,  于
于 ,在线段
,在线段 上是否存在点
上是否存在点 ,使
,使 ?若存在,求
?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.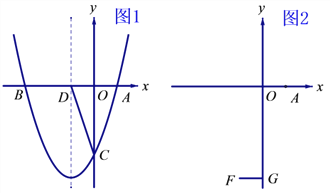
相关试题

