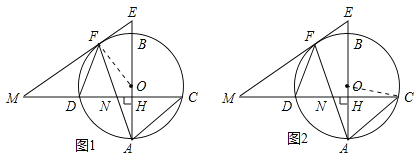
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1)求证:CA=CN;
(2)连接DF,若cos∠DFA=![]() ,AN=
,AN=![]() ,求圆O的直径的长度.
,求圆O的直径的长度.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OF,根据切线的性质结合四边形内角和为360°,即可得出∠M+∠FOH=180°,由三角形外角结合平行线的性质即可得出∠M=∠C=2∠OAF,再通过互余利用角的计算即可得出∠CAN=90°﹣∠OAF=∠ANC,由此即可证出CA=CN;
(2)连接OC,由圆周角定理结合cos∠DFA=![]() ,AN=
,AN=![]() ,即可求出CH、AH的长度,设圆的半径为r,则OH=r﹣6,根据勾股定理即可得出关于r的一元一次方程,解之即可得出r,再乘以2即可求出圆O直径的长度.
,即可求出CH、AH的长度,设圆的半径为r,则OH=r﹣6,根据勾股定理即可得出关于r的一元一次方程,解之即可得出r,再乘以2即可求出圆O直径的长度.
试题解析:(1)证明:连接OF,则∠OAF=∠OFA,如图所示.
∵ME与⊙O相切,∴OF⊥ME.∵CD⊥AB,∴∠M+∠FOH=180°.
∵∠BOF=∠OAF+∠OFA=2∠OAF,∠FOH+∠BOF=180°,∴∠M=2∠OAF.
∵ME∥AC,∴∠M=∠C=2∠OAF.
∵CD⊥AB,∴∠ANC+∠OAF=∠BAC+∠C=90°,∴∠ANC=90°﹣∠OAF,∠BAC=90°﹣∠C=90°﹣2∠OAF,∴∠CAN=∠OAF+∠BAC=90°﹣∠OAF=∠ANC,∴CA=CN.
(2)连接OC,如图2所示.
∵cos∠DFA=![]() ,∠DFA=∠ACH,∴
,∠DFA=∠ACH,∴![]() =
=![]() .设CH=4a,则AC=5a,AH=3a,∵CA=CN,∴NH=a,∴AN=
.设CH=4a,则AC=5a,AH=3a,∵CA=CN,∴NH=a,∴AN=![]() =
=![]() =
=![]() a=
a=![]() ,∴a=2,AH=3a=6,CH=4a=8.
,∴a=2,AH=3a=6,CH=4a=8.
设圆的半径为r,则OH=r﹣6,在Rt△OCH中,OC=r,CH=8,OH=r﹣6,∴OC2=CH2+OH2,r2=82+(r﹣6)2,解得:r=![]() ,∴圆O的直径的长度为2r=
,∴圆O的直径的长度为2r=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与另一腰的夹角为40°,则它的顶角的度数为度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若4x+8与﹣2x﹣10的值互为相反数,则x的值为_____.
-
科目: 来源: 题型:
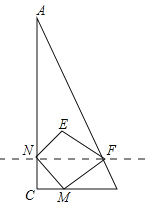
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动,在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°,再过点N作AC的垂线交AB于点F,连接MF,将△MNF关于直线NF对称后得到△ENF,已知AC=8cm,BC=4cm,设点M运动时间为t(s),△ENF与△ANF重叠部分的面积为y(cm2).
(1)在点M的运动过程中,能否使得四边形MNEF为正方形?如果能,求出相应的t值;如果不能,说明理由;
(2)求y关于t的函数解析式及相应t的取值范围;
(3)当y取最大值时,求sin∠NEF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】十八大报告指出:“建设生态文明,是关系人民福祉、关乎民族未来的长远大计”,这些年党和政府在生态文明的发展进程上持续推进,在“十一五”期间,中国减少二氧化碳排放1 460 000 000吨,赢得国际社会广泛赞誉.将1 460 000 000用科学记数法表示为( )
A.146×107
B.1.46×107
C.1.46×109
D.1.46×1010 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算2﹣3的结果为( )
A.﹣1
B.﹣2
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列算式中,正确的是( )
A.2x+3y=5xy
B.3x2+2x3=5x5
C.x3﹣x2=x
D.x2﹣3x2=﹣2x2
相关试题

