【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.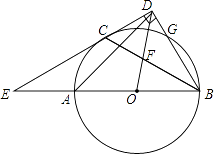
(1)求证:CD是⊙O的切线.
(2)若 ![]() ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD= ![]() ,求AD的长.
,求AD的长.
参考答案:
【答案】
(1)证明:如图1,连接OC,AC,CG,
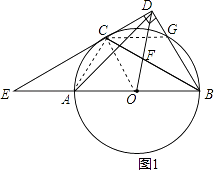
∵AC=CG,
∴ ![]() ,
,
∴∠ABC=∠CBG,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OCB=∠CBG,
∴OC∥BG,
∵CD⊥BG,
∴OC⊥CD,
∴CD是⊙O的切线
(2)解:∵OC∥BD,
∴△OCF∽△BDF,△EOC∽△EBD,
∴ ![]() ,
,
∴ ![]() ,
,
∵OA=OB,
∴AE=OA=OB,
∴OC= ![]() OE,
OE,
∵∠ECO=90°,
∴∠E=30°
(3)解:如图2,过A作AH⊥DE于H,
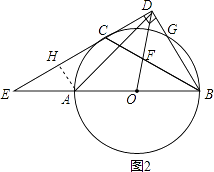
∵∠E=30°
∴∠EBD=60°,
∴∠CBD= ![]() EBD=30°,
EBD=30°,
∵CD= ![]() ,
,
∴BD=3,DE=3 ![]() ,BE=6,
,BE=6,
∴AE= ![]() BE=2,
BE=2,
∴AH=1,
∴EH= ![]() ,
,
∴DH=2 ![]() ,
,
在Rt△DAH中,AD= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)连接OC,AC,CG,由圆周角定理,得出∠ABC=∠CBG,再根据同圆的半径相等机等量代换求得∠OCB=∠CBG,根据平行线的判定得到OC∥BG,由已知CD⊥BG,得出OC⊥CD,即可证得结论。
(2)由OC∥BD,得出△OCF∽△BDF,△EOC∽△EBD,得出对应边成比例,再根据直角三角形的性质,可求出∠E的度数。
(3)过A作AH⊥DE于H,通过解直角三角形求出BD、BE、DE的长,在Rt△DAH中,根据勾股定理求出AD的长。
-
科目: 来源: 题型:
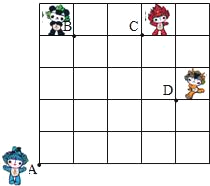
查看答案和解析>>【题目】如图,奥运福娃在5×5的方格(每个格边长尾1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:
B→A(﹣4,﹣1).请根据图中所给信息解决下列问题:
(1)A→C(______),_____);
B→C(______),_____);C→_____(﹣4,﹣3);
(2)如果贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)如果贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),
(+2,﹣1),(﹣2,+3),(﹣1,﹣1),请在图中标出妮妮的位置E点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图一,现有足够多的边长为
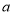 的小正方形纸片(
的小正方形纸片(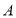 类)、长为
类)、长为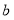 宽为
宽为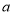 的长方形纸片(
的长方形纸片(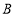 类)以及边长为
类)以及边长为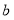 的大正方形纸片(
的大正方形纸片(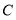 类).
类).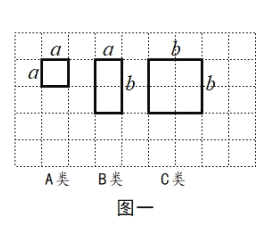
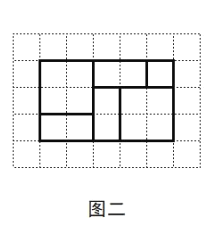
如图二,小明利用上述三种纸片各若干张,拼出了一个长为
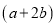 ,宽为
,宽为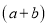 的长方形,并用这个长方形解释了等式
的长方形,并用这个长方形解释了等式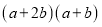
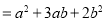 是成立的.
是成立的.(1)若取图一中的纸片若干张(三种都要取到)拼成一个长方形(所取纸片用完无剩余),使它的长和宽分别为
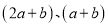 ,请你通过计算说明需要
,请你通过计算说明需要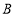 类卡片多少张;
类卡片多少张;(2)若取
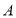 类纸片
类纸片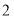 张,
张,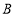 类纸片
类纸片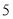 张,
张,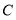 类纸片
类纸片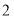 张,能拼成一个长方形吗(所取纸片用完无剩余)?请你在图三中画出示意图并在下面直接写出能用该长方形来解释成立的等式;
张,能拼成一个长方形吗(所取纸片用完无剩余)?请你在图三中画出示意图并在下面直接写出能用该长方形来解释成立的等式;

(3)如图四,大正方形的边长为
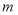 ,小正方形的边长为
,小正方形的边长为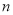 ,用四个完全相同的长方形的长和宽为别为
,用四个完全相同的长方形的长和宽为别为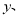
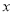 .请你通过观察或计算,判断下列
.请你通过观察或计算,判断下列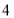 个式子是否成立,将其中成立的式子的都填写在横线上: (直接填写序号).
个式子是否成立,将其中成立的式子的都填写在横线上: (直接填写序号).①
 ;
;②
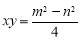 ;
;③
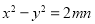 ;
;④
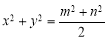 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,反比例函数y=
 (x>0)的图象上有一点A(a,3),过点A作AB⊥x轴于点B,将点B沿x轴正方向平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数于点D,CD=
(x>0)的图象上有一点A(a,3),过点A作AB⊥x轴于点B,将点B沿x轴正方向平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数于点D,CD=  ,直线AD与x轴交于点M,与y轴交于点N.
,直线AD与x轴交于点M,与y轴交于点N.
(1)用含a的式子表示点D的横坐标为:;
(2)求a的值和直线AD的函数表达式;
(3)请判断线段AN与MD的数量关系,并说明理由;
(4)若一次函数y1=k1x+b1经过点(10,9),与双曲线y= (x>0)交于点P,且该一次函数y1的值随x的增大而增大,请确定P点横坐标n的取值范围(不必写出过程)
(x>0)交于点P,且该一次函数y1的值随x的增大而增大,请确定P点横坐标n的取值范围(不必写出过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格图中小方格都是边长为1个单位长度的小正方形,已知三角形ABC的三个顶点都在网格的格点上,按要求完成下列各小题.
(1)请在图中画出将三角形ABC先向上平移1个单位长度,再向右平移3个单位长度后的图形,即三角形A′B′C′,并指出图中相等的线段;
(2)在(1)的基础上,A′B′,B′C′分别与AC交于点E,F.若∠A=50°,∠C′=51°,分别求出∠A′EF与∠B′FC的度数.
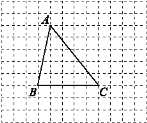
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)试探究∠2与∠3的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店3月份经营一种热销商品,每件成本20元,发现三周内售价在持续提升,销售单价P(元/件)与时间t(天)之间的函数关系为P=30+
 t(其中1≤t≤21,t为整数),且其日销售量y(件)与时间t(天)的关系如下表
t(其中1≤t≤21,t为整数),且其日销售量y(件)与时间t(天)的关系如下表 时间t(天)
1
5
9
13
17
21
日销售量y(件)
118
110
102
94
86
78
(1)已知y与t之间的变化规律符合一次函数关系,请直接写出y(件)与时间t(天)函数关系式;
(2)在这三周的销售中,第几天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的21天中,该网店每销售一件商品就捐赠a元利润(a<8)给“精准扶贫”的对象,通过销售记录发现,这21天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
相关试题

