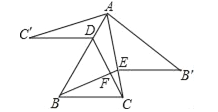
【题目】如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC',△AEB≌△AEB',且C'D∥EB'∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是_____°.(用含x的式子表示)
参考答案:
【答案】![]()
【解析】
延长C′D交AC于M,如图,根据全等的性质得∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=x,再利用三角形外角性质得∠C′MC=∠C′+∠C′AM=∠C′+2x,接着利用C′D∥B′E得到∠AEB=∠C′MC,而根据三角形内角和得到∠AEB′=180°-∠B′-x,则∠C′+2x=180°-∠B′-x,所以∠C′+∠B′=180°-3x,利用三角形外角性质和等角代换得到∠BFC=∠C=x+∠C′+∠B′,所以∠BFC=180°-2x.
延长C′D交AC于M,如图,

∵△ADC≌△ADC′,△AEB≌△AEB′,∴∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=x,
∴∠C′MC=∠C′+∠C′AM=∠C′+2x,
∵C′D∥B′E,
∴∠AEB=∠C′MC,
∵∠AEB′=180°∠B′∠B′AE=180°∠B′x,
∴∠C′+2x=180°∠B′x,
∴∠C′+∠B′=180°3x,
∵∠BFC=∠BDF+∠DBF=∠DAC+∠B′=x+∠ACD+∠B′=x+∠C′+∠B′
=x+180°3x=180°2x.
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB=20cm,CD=2cm,线段CD在线段AB上运动,E、F分别是AC、BD的中点.
(1)若AC=4cm,则EF=_______cm.
(2)当线段CD在线段AB上运动时,EF的长度是否改变,如果变化,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,作射线AE,操作结果如图所示,下列结论不能由上述操作结果得出的是( ).
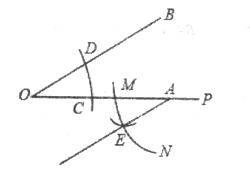
A. ∠ACD=∠EAP B. ∠ODC=∠AEM C. OB∥AE D. CD∥ME
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知双曲线y=
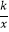 (k>0)经过Rt△OAB的直角边AB的中点C,与斜边OB相交于点D,若OD=1,则BD= .
(k>0)经过Rt△OAB的直角边AB的中点C,与斜边OB相交于点D,若OD=1,则BD= . 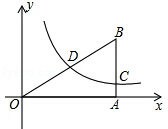
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=
 (AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
(AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.解:猜想: .
证明:

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了绿化环境,育英中学八年级三班同学都积极参加植树活动,今年植树节时,该班同学植树情况的部分数据如图所示,请根据统计图信息,回答下列问题:
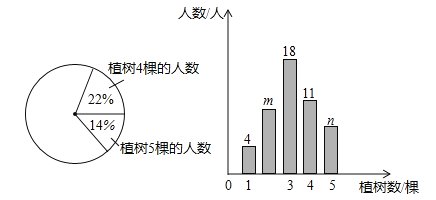
(1)八年级三班共有多少名同学?
(2)条形统计图中,m= ,n= .
(3)扇形统计图中,试计算植树2棵的人数所对应的扇形圆心角的度数.
-
科目: 来源: 题型:
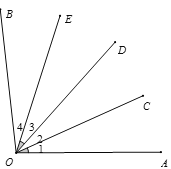
查看答案和解析>>【题目】如图所示,∠1=∠2=∠3=∠4=24°,根据图形填空:
(1)是∠2的3倍的角是_________________(用字母表示)
(2)是∠AOD的
 的角有_________个;
的角有_________个;(3)射线OC是哪个角的3等分线?又是哪个角的4等分线?
相关试题

