【题目】如图,已知等边△ABC,延长△ABC的各边分别到点D、E、F使得AE=BF=CD,顺次连接D、E、F,求证:△DEF是等边三角形.

参考答案:
【答案】见解析
【解析】
由等边三角形的性质得出∠BAC=∠ABC=∠ACB=60°,AB=BC=AC,得出∠EAF=∠FBD=∠DCE=120°,作出AF=BD=CE,证明△AEF≌△BFD≌△CDE(SAS),得出EF=FD=DE,即可得出结论.
证明:∵△ABC是等边三角形,
∴∠BAC=∠ABC=∠ACB=60°,AB=BC=AC,
∴∠EAF=∠FBD=∠DCE=120°,
∵AE=BF=CD,
∴AB+BF=BC+CD=AC+AE,
即AF=BD=CE,
在△AEF、△BFD和△CDE中, ,
,
∴△AEF≌△BFD≌△CDE(SAS),
∴EF=FD=DE,
∴△DEF是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一三角形纸片ABC,∠A=70°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两个纸片均为等腰三角形,则∠C的度数可以是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=12米,MA⊥AB于点A,MA=6米,射线BD⊥AB于点B,点P从点B出发沿BA方向往点A运动,每秒走1米,点Q从点B出发沿BD方向运动,每秒走2米,若点P、Q同时从点B出发,出发t秒后,在线段MA上有一点C,使由点C、A、P组成的三角形与△PBQ全等,则t的值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=
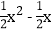 与直线
与直线 交于A、B,直线AB交于y轴于点C,点P为线段OB上一个动点(不与点O、B重合),当△OPC为等腰三角形时,点P的坐标:_______.
交于A、B,直线AB交于y轴于点C,点P为线段OB上一个动点(不与点O、B重合),当△OPC为等腰三角形时,点P的坐标:_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=60°,AD平分∠BAC,CE平分∠BCA,AD、CE交于点F,CD=CG,连结FG.

(1)求证:FD=FG;
(2)线段FG与FE之间有怎样的数量关系,请说明理由;
(3)若∠B≠60°,其他条件不变,则(1)和(2)中的结论是否仍然成立?请直接写出判断结果,不必说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
相关试题

