【题目】如图,在△ABC中,∠B=60°,AD平分∠BAC,CE平分∠BCA,AD、CE交于点F,CD=CG,连结FG.

(1)求证:FD=FG;
(2)线段FG与FE之间有怎样的数量关系,请说明理由;
(3)若∠B≠60°,其他条件不变,则(1)和(2)中的结论是否仍然成立?请直接写出判断结果,不必说明理由.
参考答案:
【答案】(1)见解析;(2)FG=FE,理由见解析;(3)(1)中结论成立.(2)中结论不成立.理由见解析
【解析】
(1)证明△CFD≌△CFG(SAS)即可解决问题;
(2)证明△AFG≌△AFE(ASA),可得FG=FE;
(3)结论:(1)中结论成立.(2)中结论不成立.
(1)证明:∵EC平分∠ACB,
∴∠FCD=∠FCG,
∵CG=CD,CF=CF,
∴△CFD≌△CFG(SAS),
∴FD=FG.
(2)结论:FG=FE.
理由:∵∠B=60°,
∴∠BAC+∠BCA=120°,
∵AD平分∠BAC,CE平分∠BCA,
∴∠ACF+∠FAC=![]() (∠BCA+∠BAC)=60°,
(∠BCA+∠BAC)=60°,
∴∠AFC=120°,∠CFD=∠AFE=60°,
∵△CFD≌△CFG,
∴∠CFD=∠CFG=60°,
∴∠AFG=∠AFE=60°,
∵AF=AF,∠FAG=∠FAE,
∴△AFG≌△AFE(ASA),
∴FG=FE.
(3)结论:(1)中结论成立.(2)中结论不成立.
理由:①同法可证△CFD≌△CFG(SAS),
∴FD=FG.
②∵∠B≠60°,
∴无法证明∠AFG=∠AFE,
∴不能判断△AFG≌△AFE,
∴(2)中结论不成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边△ABC,延长△ABC的各边分别到点D、E、F使得AE=BF=CD,顺次连接D、E、F,求证:△DEF是等边三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=
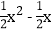 与直线
与直线 交于A、B,直线AB交于y轴于点C,点P为线段OB上一个动点(不与点O、B重合),当△OPC为等腰三角形时,点P的坐标:_______.
交于A、B,直线AB交于y轴于点C,点P为线段OB上一个动点(不与点O、B重合),当△OPC为等腰三角形时,点P的坐标:_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式及其展开式
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
…
根据下图,猜想:
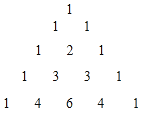
(a+b)5=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,∠B=90°,点D为直线BC上一个动点(不与B,C重合),连结AD.将线段AD绕点D按顺吋针方向旋转90°得到线段DE,连结EC.
(1)如图1,点D在线段BC上,依题意画图得到图2.
①求证:∠BAD=∠EDC;
②方方同学通过观察、测量得出结论:在点D运动的过程中,总有∠DCE=135°.方方的主要思路有以下几个:
思路一:在AB上取一点F使得BF=BD,要证∠DCE=135°,只需证△ADF≌△DEC.
思路二:以点D为圆心,DC为半径画弧交AC于点F,要证∠DCE=135°,只需证△AFD≌△ECD.
思路三:过点E作BC所在直线的垂线段EF,要证∠DCE=135°,只需证EF=CF.
……
请你参考井选择其中一个思路,证明∠DCE=135°;
(2)如果点D在线段CB的延长线上运动,利用图3画图分析,∠DCE的度数还是确定的值吗?如果是,请写出∠DCE的度数并说明理由;如果不是,也请说明你的理由.

相关试题

