【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,
,![]() .
. ![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ∥
∥![]() .
.
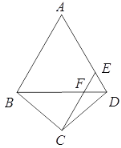
(1)求证:![]() ;
;
(2)若![]() ,
,![]() . 求
. 求![]() 的长 .
的长 .
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由等边三角形的判定定理可得△ABD为等边三角形,又由平行进行角度间的转化可得出结论.
(2)连接AC交BD于点O,由题意可证AC垂直平分BD,△ABD是等边三角形,可得∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4,通过证明△EDF是等边三角形,可得DE=EF=DF=2,由勾股定理可求OC,BC的长.
(1)证明:∵![]() ,
,![]() ,
,
∴△![]() 是等边三角形.
是等边三角形.
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() .
.
∴![]() .
.
(2)解:连接![]() 交
交![]() 于点
于点![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() 垂直平分
垂直平分![]() .
.
∴![]() .
.
∵△![]() 是等边三角形,
是等边三角形,![]()
∴![]() ,
,
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() .
.
∴![]() ,
, ![]() .
.
∵![]() .
.
∴![]() .
.
∴△![]() 是等边三角形.
是等边三角形.
∴![]() ,
,
∴![]() ,
,![]() .
.
在Rt△![]() 中,
中,
∴![]() .
.
在Rt△![]() 中,
中,
∴![]() .
.
-
科目: 来源: 题型:
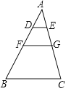
查看答案和解析>>【题目】如图,
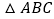 中,
中, ,且
,且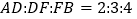 ,则
,则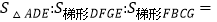 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
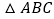 放在每个小正方形的边长为
放在每个小正方形的边长为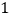 的网格中,点
的网格中,点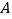 、
、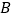 、
、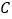 均落在格点上.
均落在格点上.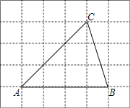
(1)
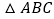 的面积等于________;
的面积等于________; 若四边形
若四边形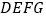 是
是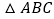 中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明)________.
中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明)________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 、
、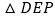 是两个全等的等腰直角三角形,
是两个全等的等腰直角三角形,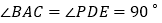 .
. 若将
若将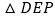 的顶点
的顶点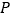 放在
放在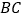 上(如图
上(如图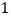 ),
),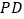 、
、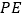 分别与
分别与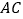 、
、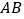 相交于点
相交于点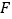 、
、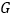 .求证:
.求证: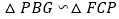 ;
; 若使
若使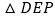 的顶点
的顶点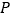 与顶点
与顶点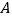 重合(如图
重合(如图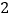 ),
),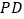 、
、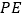 与
与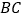 相交于点
相交于点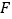 、
、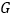 .试问
.试问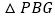 与
与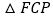 还相似吗?为什么?
还相似吗?为什么?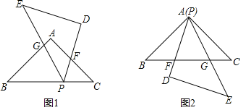
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,然后回答问题 .
已知
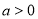 ,
,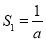 ,
,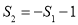 ,
, ,
,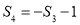 ,
,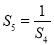 ,….,当
,….,当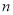 为大于1的奇数时,
为大于1的奇数时,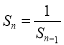 ;当
;当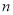 为大于1的偶数时,
为大于1的偶数时,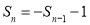 .
.(1)求
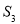 ;(用含
;(用含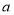 的代数式表示)
的代数式表示)(2)直接写出
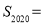 ;(用含
;(用含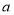 的代数式表示)
的代数式表示)(3)计算:
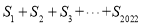 = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若一个三角形中,其中有一个内角是另外一个内角的一半,则这样的三角形叫做“半角三角形”. 例如:等腰直角三角形就是“半角三角形”.在钝角三角形
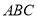 中,
中,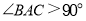 ,
,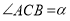 ,
,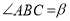 ,过点
,过点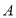 的直线
的直线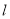 交
交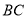 边于点
边于点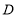 .点
.点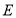 在直线
在直线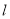 上,且
上,且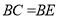 .
.(1)若
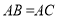 ,点
,点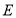 在
在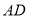 延长线上.
延长线上.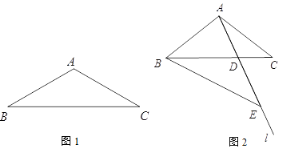
① 当
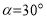 ,点
,点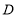 恰好为
恰好为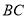 中点时,依据题意补全图1.请写出图中的一个“半角三角形”:_______;
中点时,依据题意补全图1.请写出图中的一个“半角三角形”:_______;② 如图2,若
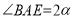 ,图中是否存在“半角三角形”(△
,图中是否存在“半角三角形”(△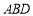 除外),若存在,请写出图中的“半角三角形”,并证明;若不存在,请说明理由;
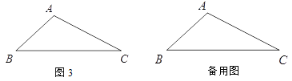
除外),若存在,请写出图中的“半角三角形”,并证明;若不存在,请说明理由;(2)如图3,若
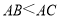 ,保持
,保持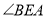 的度数与(1)中②的结论相同,请直接写出
的度数与(1)中②的结论相同,请直接写出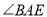 ,
,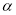 ,
,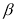 满足的数量关系:______.
满足的数量关系:______.
相关试题

