【题目】为了贯彻落实国家关于增强青少年体质的计划,我市全面实施了义务教育学段中小学学生“饮用奶计划”的营养工程.某牛奶供应商拟提供A(原味)、B(草莓味)、C(核桃味)、D(菠萝味)、E(香橙味)等五种口味的学生奶供学生选择(所有学生奶盒形状、大小相同),为了解对学生奶口味的喜好情况,某初级中学九年级(1)班张老师对全班同学进行了调查统计,制成了如图所示的两幅不完整的统计图.
(1)该班共有多少人?
(2)求出喜好A和E学生奶口味的人数;
(3)该班五种口味的学生奶喜好人数组成一组统计数据,求出这组数据的平均数;
(4)将折线统计图补充完整.

参考答案:
【答案】(1)40人;(2)喜欢A类型的人数是4人,喜欢E类型的人数是 6人 ;(3)8;(4)见解析
【解析】试题分析:
(1)结合两幅统计图可得:喜欢B种口味的有12人,占被调查人数的30%,由此可计算出全班的总人数为:12÷30%=40(人);
(2)结合(1)中所得全班总人数为40人和喜欢E种口味的占15%可计算出喜欢E种口味的有6人,结合折线统计图中已知的喜欢B、C、D三种口味的人数,即可计算出喜欢A种口味的人数;
(3)由总人数40除以5即可得到所求平均数;
(4)根据(2)中计算结果即可将折线统计图补充完整.
试题解析:
(1)根据题意得:12÷30%=40(人),
答:(1)该班共有40人;
(2)喜欢E类型的人数是:40×15%=6人,则喜欢A类型的人数是40﹣12﹣8﹣10﹣6=4人;
(3)这组数据的平均数是40÷5=8;
(4)根据(2)得出的数据可直接补图,如下:
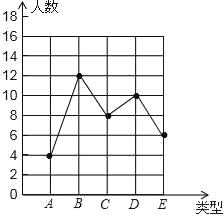
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=x-6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF//AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.
(1)①直线y=x-6与坐标轴交点坐标是A(_____,______),B(______,_____);
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);
(3)连接AD,BC四边形ABCD是什么图形,并求t为何值时,四边形ABCD的面积为36?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD中,以BF为底向正方形外侧作等腰直角三角形BEF,连接DF,取DF的中点G,连接EG,CG.

(1)如图1,当点A与点F重合时,猜想EG与CG的数量关系为 ,EG与CG的位置关系为 ,请证明你的结论.
(2)如图2,当点F在AB上(不与点A重合)时,(1)中结论是否仍然成立?请说明理由;如图3,点F在AB的左侧时,(1)中的结论是否仍然成立?直接做出判断,不必说明理由.
(3)在图2中,若BC=4,BF=3,连接EC,求
 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
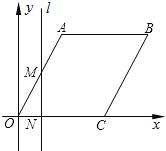
A.
 B.
B.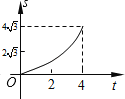
C.
 D.
D.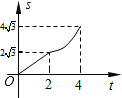
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论一定成立的是_______
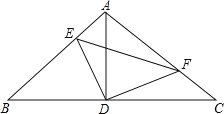
①△ADF≌△BDE
②S四边形AEDF=
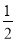 S△ABC
S△ABC③BE+CF=AD
④EF=AD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小莹用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,BC长为10cm.当小莹折叠时,顶点D落在BC边上的点F处(折痕为AE).则此时EC=( )cm
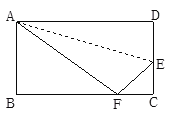
A.4B.
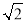 C.
C.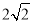 D.3
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)请用树状图或列表法求恰好选中甲、乙两位同学的概率;
(2)请利用若干个除颜色外其余都相同的乒乓球,设计一个摸球的实验(至少摸两次),
并根据该实验写出一个发生概率与(1)所求概率相同的事件.
相关试题

