【题目】如图,等边△ABC中,AB=2,AD⊥BC,以AD、CD为邻边做矩形ADCE,将△ADC绕点D顺时针旋转一定的角度得到△A′DC′使点A′落在CE上,连接AA′,CC′.
(1)求AD的长;
(2)求证:△ADA′∽△CDC′;
(3)求CC′2的值.

参考答案:
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)利用等边三角形的性质得出∠DAB=30°,进而求出BD,即可得出结论;
(2)先判断出![]() ,即可得出结论;
,即可得出结论;
(3)先求出A'C,A'E,进而利用勾股定理求出A'A2,即可得出结论.
(1)∵AD是等边三角形ABC的高,
∴∠B=60°,∠ADB=90°,
∴∠DAB=30°,
∵AB=2,∴BD=![]() AB=1,
AB=1,
∴AD=![]() ;
;
(2)由旋转知,AD=A'D,CD=C'D,
∴![]() ,
,
由旋转知,∠ADA'=∠CDC',
∴△ADA'∽△CDC';
(3)在矩形ABCD中,∠DCE=90°,A'D=AD=![]() ,AE=CD=1,
,AE=CD=1,
∴A'C=![]() ,
,
∴A'E=CE﹣A'C=AD﹣A'C=![]() ,
,
在Rt△AEA'中,A'A2=A'E2+A'E2=(![]() )2+12=6﹣2
)2+12=6﹣2![]() ,
,
∵△ADA'∽△CDC',
∴![]() ,
,
∴CC'2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的结论是( )

A.CD=DN;B.∠1=∠2;C.BE=CF;D.△ACN≌△ABM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°②∠ADE=∠CDE③DE=BE④AD=AB+CD,四个结论中成立的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正确的个数有( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
 (k≠0)的图象交于第一、三象限内的两点A、B,与y轴交于C点.过点A作AD⊥y轴,垂足为点D,AD=8,OC=2,tan∠ACD=2.点B的坐标为(m,﹣4).
(k≠0)的图象交于第一、三象限内的两点A、B,与y轴交于C点.过点A作AD⊥y轴,垂足为点D,AD=8,OC=2,tan∠ACD=2.点B的坐标为(m,﹣4).(1)求该反比例函数和一次函数的解析式;
(2)直接写出当x取何值时,ax+b﹣
 >0成立.
>0成立.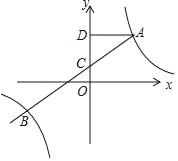
-
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)该班共有_____名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为_____;
(4)学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线相交于点A1,得∠A1;∠A1BC和∠A1CD的平分线相交于点A2,得∠A2;…;∠A2018BC和∠A2018CD的平分线交于点A2019,则∠A2019=________度.

相关试题

