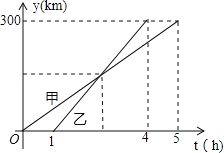
【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时; ③乙车出发后2小时追上甲车; ④当甲、乙两车相距50千米时,t=![]() 或
或![]() .其中正确的结论有_____.
.其中正确的结论有_____.
参考答案:
【答案】①②
【解析】
观察图象可判断①②,由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,可求得两函数图象的交点,可判断③,再令两函数解析式的差为50,可求得t,可判断④,可得出答案.
由图象可知,A、B两城市之间的距离为300km,甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,
∴①②都正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得,k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得
![]() ,
,
解得![]() ,
,
∴y乙=100t﹣100,
令y甲=y乙可得:60t=100t﹣100,
解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,
∴③不正确;
令|y甲﹣y乙|=50,可得|60t﹣100t+100|=50,即|100﹣40t|=50,
当100﹣40t=50时,可解得t=![]() ,
,
当100﹣40t=﹣50时,可解得t=![]() ,
,
又当t=![]() 时,y甲=50,此时乙还没出发,
时,y甲=50,此时乙还没出发,
当t=![]() 时,乙到达B城,y甲=250;
时,乙到达B城,y甲=250;
综上可知当t的值为![]() 或
或![]() 或
或![]() 或t=
或t=![]() 时,两车相距50千米,
时,两车相距50千米,
∴④不正确;
综上,正确的有①②,
故答案为:①②
-
科目: 来源: 题型:
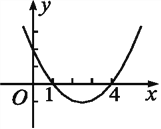
查看答案和解析>>【题目】已知二次函数y=ax2-5x+c的图象如图所示.
(1)试求该二次函数的解析式和它的图象的顶点坐标;
(2)观察图象回答,x何值时y的值大于0?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为培养学生的特长爱好,提髙学生的综合素质,某校音乐特色学习班准备从京东商城里一次性购买若干个尤克里里和竖笛(每个尤克里里的价格相同,每个竖笛的价格相同),购买2个竖笛和1个尤克里里共需290元;竖笛单价比尤克里里单价的一半少25元.
(1)求竖笛和尤克里里的单价各是多少元?
(2)根据学校实际情况,需一次性购买竖笛和尤克里里共20个,但要求购买竖笛和尤克里里的总费用不超过3450元,则该校最多可以购买多少个尤克里里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且mn
 0)的大致图像是( )
0)的大致图像是( )A.
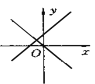 B.
B.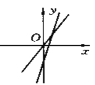
C.
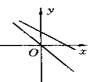 D.
D.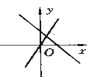
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于X的一元二次方程为:
 。
。(1)当方程有两实数根时,求
 的取值范围;
的取值范围;(2)任取一个
 值,求出方程的两个不相等实数根。
值,求出方程的两个不相等实数根。 -
科目: 来源: 题型:
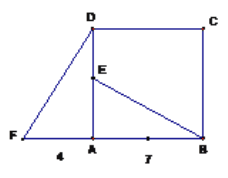
查看答案和解析>>【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7.
(1)旋转中心是点 ,旋转了 度,DE的长度是 ;
(2)BE与DF的关系如何? 请说明理由.(提示:延长BE交DF于点G)
-
科目: 来源: 题型:
查看答案和解析>>【题目】依据给定的条件,求一次函数的表达式.
(1)已知一次函数的图象如图所示,求此一次函数的表达式,并判断点(6,5)是否在此函数图象上;
(2)已知直线y=kx+b平行于直线y=3x+4,且过点(1,2),求此直线的函数表达式.

相关试题

