【题目】如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.

将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数 | 1 | 3 | 6 | 10 | 15 | 21 | a | … |
正方形数 | 1 | 4 | 9 | 16 | 25 | b | 49 | … |
五边形数 | 1 | 5 | 12 | 22 | c | 51 | 70 | … |
(1)按照规律,表格中a= ,b= ,c= .
(2)观察表中规律,第n个“正方形数”是 ;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是 .
参考答案:
【答案】(1)见解析(2)见解析
【解析】
(1)首先根据前6个“三角形数”分别是1=![]() 、3=
、3=![]() 、6=
、6=![]() 、10=
、10=![]() 、15=
、15=![]() 、21=
、21=![]() ,可得第n个“三角形数”是
,可得第n个“三角形数”是![]() ,据此求出a的值是多少;然后根据前5个“正方形数”分别是1=12,4=22,9=32,16=42,25=52,可得第n个“正方形数”是n2,据此求出b的值是多少;最后根据前4个“五边形数”分别是1=
,据此求出a的值是多少;然后根据前5个“正方形数”分别是1=12,4=22,9=32,16=42,25=52,可得第n个“正方形数”是n2,据此求出b的值是多少;最后根据前4个“五边形数”分别是1=![]() ,5=
,5=![]() ,12=
,12=![]() ,22=
,22=![]() ,可得第n个“五边形数”是
,可得第n个“五边形数”是![]() ,据此求出c的值是多少即可.
,据此求出c的值是多少即可.
(2)首先判断出第n个“正方形数”是n2;然后分别求出第1个“三角形数”、第1个“正方形数”的和与第1个“五边形数”的差是多少,第2个“三角形数”、第2个“正方形数”的和与第2个“五边形数”的差是多少;第3个“三角形数”、第3个“正方形数”的和与第3个“五边形数”的差是多少;最后总结出规律,用含x、n的代数式表示第n个“五边形数”即可.
(1)∵前6个“三角形数”分别是:
1=![]() 、3=
、3=![]() 、6=
、6=![]() 、10=
、10=![]() 、15=
、15=![]() 、21=
、21=![]() ,
,
∴第n个“三角形数”是![]() ,
,
∴a=![]() =28.
=28.
∵前5个“正方形数”分别是:
1=12,4=22,9=32,16=42,25=52,
∴第n个“正方形数”是n2,
∴b=62=36.
∵前4个“正方形数”分别是:
1=![]() ,5=
,5=![]() ,12=
,12=![]() ,22=
,22=![]() ,
,
∴第n个“五边形数”是![]() ,
,
∴c=![]() =35.
=35.
(2)第n个“正方形数”是n2;
1+1-1=1,
3+4-5=2,
6+9-12=3,
10+16-22=4,
…,
∴第n个“五边形数”是n2+x-n.
故答案为:28、36、35;n2、n2+x-n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级(1)班班主任对本班学生进行了“我最喜欢的课外活动”的调查,并将调查结果分为书法和绘画类(记为A)、音乐类(记为B)、球类(记为C)、其它类(记为D).根据调查结果发现该班每个学生都进行了登记且每人只登记了一种自己最喜欢的课外活动.班主任根据调查情况把学生进行了归类,并制作了如下两幅统计图.请你结合图中所给信息解答下列问题:
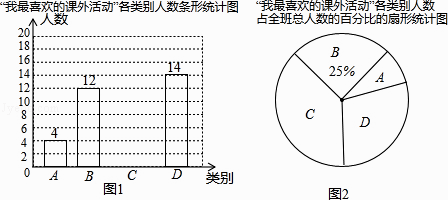
(1)七年级(1)班学生总人数为人,扇形统计图中D类所对应扇形的圆心角为度,请补全条形统计图;
(2)学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名学生擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2sin45°﹣3﹣2+
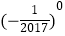 +|
+| 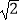 ﹣2|+
﹣2|+ 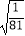 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2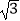 +3
+3 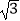 =5
=5 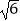
B.(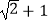 )(1﹣
)(1﹣ 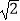 )=1
)=1
C.(xy)﹣1( xy)2=
xy)2=  xy
xy
D.﹣(﹣a)4÷a2=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,写出求BE的长的思路.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一束光线与水平面成60°的角度照射地面,现在地面AB上支放一个平面镜CD,使这束光线经过平面镜反射后成水平光线,则平面镜CD与地面AB所成角∠DCB的度数等于( )
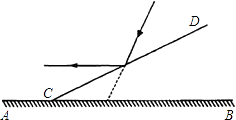
A.30°
B.45°
C.50°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人5次射击命中的环数如下:
甲
7
9
8
6
10
乙
7
8
9
8
8
则以下判断中正确的是( )
A. 甲=
甲=  乙 , S甲2=S乙2 .
乙 , S甲2=S乙2 .
B. 甲=
甲=  乙 , S甲2>S乙2 .
乙 , S甲2>S乙2 .
C. 甲=
甲=  乙 , S甲2<S乙2 .
乙 , S甲2<S乙2 .
D. 甲<
甲<  乙 , S甲2<S乙2 .
乙 , S甲2<S乙2 .
相关试题

