【题目】如图,一束光线与水平面成60°的角度照射地面,现在地面AB上支放一个平面镜CD,使这束光线经过平面镜反射后成水平光线,则平面镜CD与地面AB所成角∠DCB的度数等于( ) 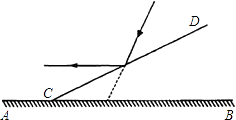
A.30°
B.45°
C.50°
D.60°
参考答案:
【答案】A
【解析】解:∵入射角等于反射角, ∴∠1=∠2,
∵光线经过平面镜CD反射后成水平光线平行,
∴∠2=∠4,
又∵∠1=∠3(对顶角相等),
∴∠3=∠4,
∴∠2=∠3,
∵光线与水平面成60°的角度照射地面,
∴∠3=60°÷2=30°,
∴∠4=30°,即∠DCB=30°.
故选A.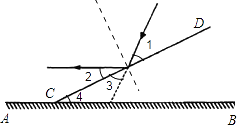
【考点精析】本题主要考查了平行线的性质和三角形的内角和外角的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2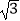 +3
+3 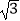 =5
=5 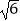
B.(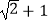 )(1﹣
)(1﹣ 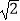 )=1
)=1
C.(xy)﹣1( xy)2=
xy)2=  xy
xy
D.﹣(﹣a)4÷a2=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.

将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数
1
3
6
10
15
21
a
…
正方形数
1
4
9
16
25
b
49
…
五边形数
1
5
12
22
c
51
70
…
(1)按照规律,表格中a= ,b= ,c= .
(2)观察表中规律,第n个“正方形数”是 ;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,写出求BE的长的思路.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人5次射击命中的环数如下:
甲
7
9
8
6
10
乙
7
8
9
8
8
则以下判断中正确的是( )
A. 甲=
甲=  乙 , S甲2=S乙2 .
乙 , S甲2=S乙2 .
B. 甲=
甲=  乙 , S甲2>S乙2 .
乙 , S甲2>S乙2 .
C. 甲=
甲=  乙 , S甲2<S乙2 .
乙 , S甲2<S乙2 .
D. 甲<
甲<  乙 , S甲2<S乙2 .
乙 , S甲2<S乙2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,把表示数1的点称为基准点,记作点
 . 对于两个不同的M和N,若点M、点N到点
. 对于两个不同的M和N,若点M、点N到点 的距离相等,则称点M与点N互为基准变换点. 例如:图中,点M表示数
的距离相等,则称点M与点N互为基准变换点. 例如:图中,点M表示数 ,点N表示数3,它们与基准点
,点N表示数3,它们与基准点 的距离都是2个单位长度,点M与点N互为基准变换点.
的距离都是2个单位长度,点M与点N互为基准变换点.
(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
① 若a=0,则b= ;若
 ,则b= ;
,则b= ;② 用含a的式子表示b,则b= ;
(2)对点A进行如下操作:先把点A表示的数乘以
 ,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是 ;
,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是 ;(3)点P在点Q的左边,点P与点Q之间的距离为8个单位长度.对P、Q两点做如下操作:点P沿数轴向右移动k(k>0)个单位长度得到
 ,
,  为
为 的基准变换点,点
的基准变换点,点 沿数轴向右移动k个单位长度得到
沿数轴向右移动k个单位长度得到 ,
,  为
为 的基准变换点,……,依此顺序不断地重复,得到
的基准变换点,……,依此顺序不断地重复,得到 ,
,  ,…,
,…,  .
.  为Q的基准变换点,将数轴沿原点对折后
为Q的基准变换点,将数轴沿原点对折后 的落点为
的落点为 ,
,  为
为的基准变换点, 将数轴沿原点对折后
 的落点为
的落点为 ,……,依此顺序不断地重复,得到
,……,依此顺序不断地重复,得到 ,
,  ,…,
,…,  .若无论k为何值,
.若无论k为何值,  与
与 两点间的距离都是4,则n= .
两点间的距离都是4,则n= . -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
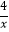 和y=
和y= 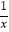 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y= 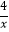 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y= 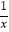 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=  AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( ) 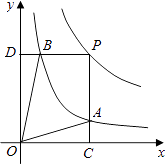
A.①②③
B.②③④
C.①③④
D.①②④
相关试题

