【题目】如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,写出求BE的长的思路.

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】(1)由平行四边形性质得AB∥CD, 可得∠ABC+∠BCD=180°,又BE,CF分别是∠ABC,∠BCD的平分线,所以∠EBC+∠FCB=90°,可得∠BGC=90°;
(2)作EH∥AB交BC于点H,连接AH交BE于点P.证四边形ABHE是菱形,可知AH,BE互相垂直平分,在Rt△ABP中,由勾股定理可求BP,进而可求BE的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∴∠ABC+∠BCD=180°.
∵BE,CF分别是∠ABC,∠BCD的平分线,
∴∠EBC=![]() ∠ABC,∠FCB=
∠ABC,∠FCB=![]() ∠BCD.
∠BCD.
∴∠EBC+∠FCB=90°.
∴∠BGC=90°.
即BE⊥CF.
(2)求解思路如下:
a.如图,作EH∥AB交BC于点H,连接AH交BE于点P.
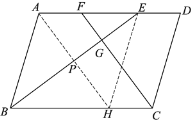
b.由BE平分∠ABC,可证AB=AE,进而可证四边形ABHE是菱形,可知AH,BE互相垂直平分;
c.由BE⊥CF,可证AH∥CF,进而可证四边形AHCF是平行四边形,可求AP=![]() ;
;
d.在Rt△ABP中,由勾股定理可求BP,进而可求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2sin45°﹣3﹣2+
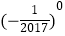 +|
+| 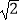 ﹣2|+
﹣2|+ 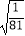 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2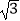 +3
+3 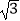 =5
=5 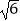
B.(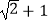 )(1﹣
)(1﹣ 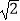 )=1
)=1
C.(xy)﹣1( xy)2=
xy)2=  xy
xy
D.﹣(﹣a)4÷a2=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,…,称为“三角形数”;把1、4、9、16,25,…称为“正方形数”.同样的,可以把数1,5,12,22,…,等数称为“五边形数”.

将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数
1
3
6
10
15
21
a
…
正方形数
1
4
9
16
25
b
49
…
五边形数
1
5
12
22
c
51
70
…
(1)按照规律,表格中a= ,b= ,c= .
(2)观察表中规律,第n个“正方形数”是 ;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一束光线与水平面成60°的角度照射地面,现在地面AB上支放一个平面镜CD,使这束光线经过平面镜反射后成水平光线,则平面镜CD与地面AB所成角∠DCB的度数等于( )
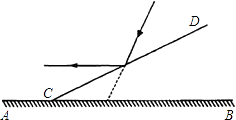
A.30°
B.45°
C.50°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人5次射击命中的环数如下:
甲
7
9
8
6
10
乙
7
8
9
8
8
则以下判断中正确的是( )
A. 甲=
甲=  乙 , S甲2=S乙2 .
乙 , S甲2=S乙2 .
B. 甲=
甲=  乙 , S甲2>S乙2 .
乙 , S甲2>S乙2 .
C. 甲=
甲=  乙 , S甲2<S乙2 .
乙 , S甲2<S乙2 .
D. 甲<
甲<  乙 , S甲2<S乙2 .
乙 , S甲2<S乙2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,把表示数1的点称为基准点,记作点
 . 对于两个不同的M和N,若点M、点N到点
. 对于两个不同的M和N,若点M、点N到点 的距离相等,则称点M与点N互为基准变换点. 例如:图中,点M表示数
的距离相等,则称点M与点N互为基准变换点. 例如:图中,点M表示数 ,点N表示数3,它们与基准点
,点N表示数3,它们与基准点 的距离都是2个单位长度,点M与点N互为基准变换点.
的距离都是2个单位长度,点M与点N互为基准变换点.
(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
① 若a=0,则b= ;若
 ,则b= ;
,则b= ;② 用含a的式子表示b,则b= ;
(2)对点A进行如下操作:先把点A表示的数乘以
 ,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是 ;
,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是 ;(3)点P在点Q的左边,点P与点Q之间的距离为8个单位长度.对P、Q两点做如下操作:点P沿数轴向右移动k(k>0)个单位长度得到
 ,
,  为
为 的基准变换点,点
的基准变换点,点 沿数轴向右移动k个单位长度得到
沿数轴向右移动k个单位长度得到 ,
,  为
为 的基准变换点,……,依此顺序不断地重复,得到
的基准变换点,……,依此顺序不断地重复,得到 ,
,  ,…,
,…,  .
.  为Q的基准变换点,将数轴沿原点对折后
为Q的基准变换点,将数轴沿原点对折后 的落点为
的落点为 ,
,  为
为的基准变换点, 将数轴沿原点对折后
 的落点为
的落点为 ,……,依此顺序不断地重复,得到
,……,依此顺序不断地重复,得到 ,
,  ,…,
,…,  .若无论k为何值,
.若无论k为何值,  与
与 两点间的距离都是4,则n= .
两点间的距离都是4,则n= .
相关试题

