【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 |
| 1 | 2 | 3 | 4 | 5 | … |
y | … |
|
|
|
| 3 |
|
|
| m | … |
求m的值;
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .
参考答案:
【答案】(1)x≠0(2)![]() (3)见解析(4)见解析
(3)见解析(4)见解析
【解析】
(1)根据分母不为零分式有意义,可得答案;
(2)根据自变量与函数值得对应关系,可得答案;
(3)根据描点法画函数图象,可得答案;
(4)根据图象的变化趋势,可得答案;
(1)x≠0 ;
(2)当![]() 时,
时,![]() .
.
∴![]()
(3)该函数的图象如下图所示.
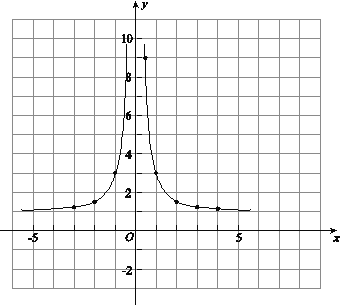
(4)该函数的其它性质:
①当x<0时,y随x的增大而增大;
当x>0时,y随x的增大而减小 .
②函数的图象与y轴无交点,图象由两部分组成 .(写出一条即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠CAB=60,BC的长为
 ,求四边形OCED的周长
,求四边形OCED的周长
-
科目: 来源: 题型:
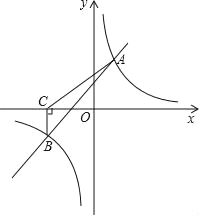
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
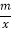 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b>
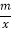 的解集;
的解集;(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某年级共有200名学生.为了解该年级学生A课程的学习情况,从中随机抽取40名学生进行测试(测试成绩是百分制,且均为正整数), 并对数据(A课程测试成绩)进行整理、描述和分析.这组数据(A课程测试成绩)的平均分数是78.38. 下表是随机抽取的40名学生A课程测试成绩频数分布表
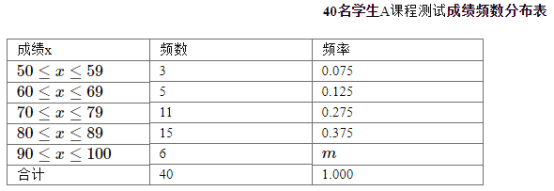
根据以上信息,回答下列问题:
(1)写出表中
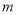 的值;
的值;(2)80分及以上的频数之和是21,79分及以下的频数之和是19,而平均分数(78.38)在80分以下. 由此可知,这次测验的成绩高于平均分的人数________(填“多”或“少”),低于平均分的人数________(填“多”或“少”),成绩属偏________(填“高”或“低”)分布;
(3)假设该年级学生都参加此次测试,估计这次A课程测试成绩90分及以上的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,A, B是直线l上的两点,点B关于AD的对称点为M,连接
 交AD于F点.
交AD于F点.(1)若
 ,如图,
,如图,①依题意补全图形;
②判断MF与FC的数量关系是 ;

(2)如图,当
 时,
时, ,CD的延长线相交于点E,取
,CD的延长线相交于点E,取 E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.
E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1:
 :3,求∠AED的度数;
:3,求∠AED的度数;(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=
 ,求CN的长.
,求CN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克)
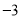
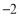
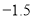
0
1
2.5
筐数
1
4
2
3
2
8
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?(结果保留整数)
相关试题

