【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是菱形ABCD的中心;
②当x= ![]() 时,EF+GH>AC;
时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是 ![]() ;
;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确结论是 . (填序号)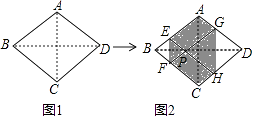
参考答案:
【答案】①④
【解析】解:∵菱形ABCD的边长为2,
∴AB=BC=2,
∵∠ABC=60°,
∴AC=AB=2,BD=2 ![]() ,
,
由折叠知,△BEF是等边三角形,
当x=1时,则AE=1,
∴BE=AB﹣AE=1,
由折叠知,BP=2× ![]() =
= ![]() =
= ![]() BD,
BD,
∴点P是菱形ABCD的对角线的交点,
即:点P是菱形ABCD的中心,所以①正确,
如图,
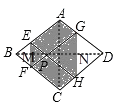
∵AE=x,
∴BE=AB﹣AE=2﹣x,
∵△BEF是等边三角形,
∴EF=BE=2﹣x,
∴BM= ![]() EM=
EM= ![]() ×
× ![]() EF=
EF= ![]() (2﹣x),
(2﹣x),
∴BP=2BM= ![]() (2﹣x),
(2﹣x),
∴DP=BD﹣BP=2 ![]() ﹣
﹣ ![]() (2﹣x)=
(2﹣x)= ![]() x,
x,
∴DN= ![]() DP=
DP= ![]() x,
x,
∴GH=2GN=2× ![]() x=x,
x=x,
当x= ![]() 时,AE=
时,AE= ![]() ,
,
∴BE=AB﹣AE= ![]() ,
,
∵△BEF是等边三角形,
∴EF=BE= ![]() ,BP=
,BP= ![]() ,
,
∴DP= ![]() ,
,
∴GH=DG= ![]() ,
,
∴EF+GH=2=AC,所以②错误;
当0<x<2时,
∵AE=x,
∴BE=2﹣x,
∴EF=2﹣x,
∴BP= ![]() (2﹣x),
(2﹣x),
∴DP= ![]() x,
x,
∴GH=2× ![]() =x=DG=DH,
=x=DG=DH,
∴六边形AEFCHG面积=S菱形ABCD﹣S△BEEF﹣S△DGH
= ![]() ×2×2
×2×2 ![]() ﹣
﹣ ![]() (2﹣x)2﹣
(2﹣x)2﹣ ![]() x2
x2
=2 ![]() ﹣
﹣ ![]() (x﹣1)2﹣
(x﹣1)2﹣ ![]()
=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
∴当x=1时,六边形AEFCHG面积最大为 ![]() ,所以③错误,
,所以③错误,
六边形AEFCHG周长=AE+EF+FC+CH+HG+AG
=x+2﹣x+x+2﹣x+x+2﹣x=6是定值,
所以④正确,即:正确的有①④,
所以答案是①④.
【考点精析】关于本题考查的二次函数的最值和菱形的性质,需要了解如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
某“综合与实践”小组开展了“长方体纸盒的制作”实践活动,他们利用边长为
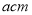 的正方形纸板制作出两种不同方案的长方体盒子(图1为无盖的长方体纸盒,图2为有盖的长方体纸盒),请你动手操作验证并完成任务.(纸板厚度及接缝处忽略不计)
的正方形纸板制作出两种不同方案的长方体盒子(图1为无盖的长方体纸盒,图2为有盖的长方体纸盒),请你动手操作验证并完成任务.(纸板厚度及接缝处忽略不计)动手操作一:
根据图1方式制作一个无盖的长方体盒子.方法:先在纸板四角剪去四个同样大小边长为
 的小正方形,再沿虚线折合起来.
的小正方形,再沿虚线折合起来.
问题解决
(1)该长方体纸盒的底面边长为_______
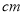 ;(请你用含
;(请你用含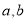 的代数式表示)
的代数式表示)(2)若
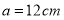 ,
, ,则长方体纸盒的底面积为_______
,则长方体纸盒的底面积为_______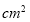 ;
;动手操作二:
根据图2方式制作一个有盖的长方体纸盒.方法:先在纸板四角剪去两个同样大小边长为
 的小正方形和两个同样大小的小长方形,再沿虚线折合起来.
的小正方形和两个同样大小的小长方形,再沿虚线折合起来.拓展延伸
(3)该长方体纸盒的体积为______
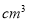 ;(请你用含
;(请你用含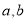 的代数式表示)
的代数式表示)(4)现有两张边长
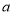 均为
均为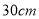 的正方形纸板,分别按图1、图2的要求制作无盖和有盖的两个长方体盒子,若
的正方形纸板,分别按图1、图2的要求制作无盖和有盖的两个长方体盒子,若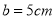 ,求无盖盒子的体积是有盖盒子体积的多少倍.
,求无盖盒子的体积是有盖盒子体积的多少倍. -
科目: 来源: 题型:
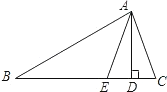
查看答案和解析>>【题目】在△ABC中,AD是BC边上的高,AE是角平分线,∠B=30°,∠C=70°,求∠CAD和∠DAE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示,将△ABC水平向左平移3个单位,再竖直向下平移2个单位。
(1)读出△ABC的三个顶点坐标;
(2)请画出平移后的△A′B′C′,并直接写出点A/、B′、C′的坐标;
(3)求平移以后的图形的面积 。

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,问A型节能灯最多可以买多少只?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的表格是某次篮球联赛部分球队的积分表,则下列说法不正确的是( )
队名
比赛场数
胜场
负场
积分
前进
14
10
4
24
光明
14
9
5
23
远大
14
7
a
21
卫星
14
4
10
b
钢铁
14
0
14
14
…
…
…
…
…
A.负一场积1分,胜一场积2分B.卫星队总积分b=18
C.远大队负场数a=7D.某队的胜场总积分可以等于它的负场总积分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形纸片ABCD,点E在边AB上,点F、G在边CD上,连接EF、EG.将∠BEG对折,点B落在直线EG上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
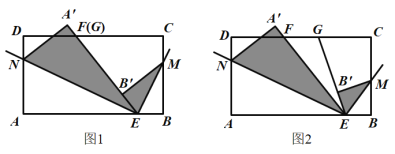
(1)如图1,若点F与点G重合,求∠MEN的度数;
(2)如图2,若点G在点F的右侧,且∠FEG=30°,求∠MEN的度数;
(3)若∠MEN=α,请直接用含α的式子表示∠FEG的大小.
相关试题

