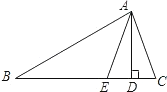
[题目]在△ABC中.AD是BC边上的高.AE是角平分线.∠B=30°.∠C=70°.求∠CAD和∠DAE的度数．题目和参考答案 ——青夏教育精英家教网—

【题目】在△ABC中，AD是BC边上的高，AE是角平分线，∠B=30°，∠C=70°，求∠CAD和∠DAE的度数．

参考答案：

【答案】∠CAD=20°, ∠DAE=20°

【解析】

在Rt△ACD中，利用直角三角形两锐角互余即可求出∠CAD；
根据三角形的内角和等于180°列式求出∠BAC，再根据角平分线的定义求出∠CAE，然后列式计算即可求出∠DAE．

解：∵AD是BC边上的高

∴∠ADC=90°

在Rt△ADC中，∠C=70°

∴∠CAD=90°-∠C=90°-70°=20°

在△ABC中

∵∠B=30°，∠C=70°

∴∠BAC=180°-∠B-∠C=180°-30°-70°=80°

∵AE平分∠BAC

∴∠CAE=∠BAC=×80°=40°

∴∠DAE=∠CAE﹣∠CAD=40°﹣20°=20°

相关试题

科目： 来源： 题型：

【题目】甲、乙两车从A地开往B地，全程800km；所行的路程与时间的函数图像如图所示，下列问题：①乙车比甲车早出发2h；②甲车追上乙车时行驶了300km；③乙车的速度小于甲车速度；④甲车跑完全程比乙车跑完全程少用3h；以上正确的序号是_______.
查看答案和解析>>
科目： 来源： 题型：

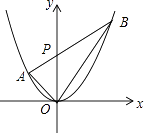
【题目】若三角形的一边和该边上的高相等的三角形称为“和谐三角形”，如图，已知抛物线y=ax2经过A（﹣1，1），P是y轴正半轴上的动点，射线AP与抛物线交于另一点B，当△AOP是“和谐三角形”时，点B的坐标为．
查看答案和解析>>
科目： 来源： 题型：

【题目】综合与实践
某“综合与实践”小组开展了“长方体纸盒的制作”实践活动，他们利用边长为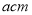的正方形纸板制作出两种不同方案的长方体盒子（图1为无盖的长方体纸盒，图2为有盖的长方体纸盒），请你动手操作验证并完成任务.（纸板厚度及接缝处忽略不计）
动手操作一：
根据图1方式制作一个无盖的长方体盒子.方法：先在纸板四角剪去四个同样大小边长为的小正方形，再沿虚线折合起来．
问题解决
（1）该长方体纸盒的底面边长为_______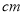；（请你用含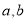的代数式表示）
（2）若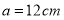，，则长方体纸盒的底面积为_______；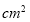
动手操作二：
根据图2方式制作一个有盖的长方体纸盒．方法：先在纸板四角剪去两个同样大小边长为的小正方形和两个同样大小的小长方形，再沿虚线折合起来．
拓展延伸
（3）该长方体纸盒的体积为______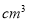；（请你用含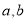的代数式表示）
（4）现有两张边长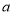均为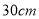的正方形纸板，分别按图1、图2的要求制作无盖和有盖的两个长方体盒子，若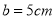，求无盖盒子的体积是有盖盒子体积的多少倍．
查看答案和解析>>
科目： 来源： 题型：

【题目】在平面直角坐标系中，△ABC的三个顶点的位置如图所示，将△ABC水平向左平移3个单位，再竖直向下平移2个单位。
（1）读出△ABC的三个顶点坐标；
（2）请画出平移后的△A′B′C′，并直接写出点A/、B′、C′的坐标；
（3）求平移以后的图形的面积。
查看答案和解析>>
科目： 来源： 题型：

【题目】如图1，菱形纸片ABCD的边长为2，∠ABC=60°，翻折∠B，∠D，使点B，D两点重合于对角线BD上一点P，EF，GH分别是折痕（如图2）．设AE=x（0＜x＜2），给出下列判断：
①当x=1时，点P是菱形ABCD的中心；
②当x= 时，EF+GH＞AC；
③当0＜x＜2时，六边形AEFCHG面积的最大值是；
④当0＜x＜2时，六边形AEFCHG周长的值不变．
其中正确结论是．（填序号）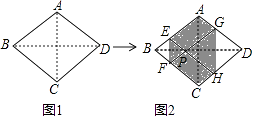
查看答案和解析>>
科目： 来源： 题型：

【题目】学校准备购进一批节能灯，已知1只A型节能灯和3只B型节能灯共需26元；3只A型节能灯和2只B型节能灯共需29元.
（1）求一只A型节能灯和一只B型节能灯的售价各是多少元；
（2）学校准备购进这两种型号的节能灯共50只，并且A型节能灯的数量不多于B型节能灯数量的3倍，问A型节能灯最多可以买多少只？
查看答案和解析>>