【题目】已知长方形纸片ABCD,点E在边AB上,点F、G在边CD上,连接EF、EG.将∠BEG对折,点B落在直线EG上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
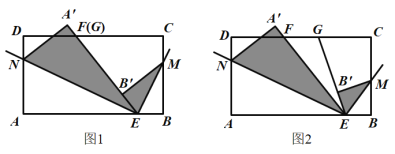
(1)如图1,若点F与点G重合,求∠MEN的度数;
(2)如图2,若点G在点F的右侧,且∠FEG=30°,求∠MEN的度数;
(3)若∠MEN=α,请直接用含α的式子表示∠FEG的大小.
参考答案:
【答案】(1)∠MEN=90°;(2)∠MEN=105°;(3)∠FEG=2α﹣180°,∠FEG=180°﹣2α.
【解析】
(1)根据角平分线的定义,平角的定义,角的和差定义计算即可.
(2)根据∠MEN=∠NEF+∠FEG+∠MEG,求出∠NEF+∠MEG即可解决问题.
(3)分两种情形分别讨论求解.
(1)∵EN平分∠AEF,EM平分∠BEF
∴∠NEF=![]() ∠AEF,∠MEF=
∠AEF,∠MEF=![]() ∠BEF
∠BEF
∴∠MEN=∠NEF+∠MEF=![]() ∠AEF+
∠AEF+![]() ∠BEF=
∠BEF=![]() (∠AEF+∠BEF)=
(∠AEF+∠BEF)=![]() ∠AEB
∠AEB
∵∠AEB=180°
∴∠MEN=![]() ×180°=90°
×180°=90°
(2)∵EN平分∠AEF,EM平分∠BEG
∴∠NEF=![]() ∠AEF,∠MEG=
∠AEF,∠MEG=![]() ∠BEG
∠BEG
∴∠NEF+∠MEG=![]() ∠AEF+
∠AEF+![]() ∠BEG=
∠BEG=![]() (∠AEF+∠BEG)=
(∠AEF+∠BEG)=![]() (∠AEB﹣∠FEG)
(∠AEB﹣∠FEG)
∵∠AEB=180°,∠FEG=30°
∴∠NEF+∠MEG=![]() (180°﹣30°)=75°
(180°﹣30°)=75°
∴∠MEN=∠NEF+∠FEG+∠MEG=75°+30°=105°
(3)若点G在点F的右侧,∠FEG=2α﹣180°,
若点G在点F的左侧侧,∠FEG=180°﹣2α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是菱形ABCD的中心;
②当x= 时,EF+GH>AC;
时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是 ;
;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确结论是 . (填序号)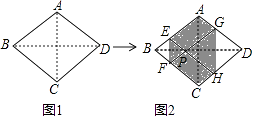
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,问A型节能灯最多可以买多少只?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的表格是某次篮球联赛部分球队的积分表,则下列说法不正确的是( )
队名
比赛场数
胜场
负场
积分
前进
14
10
4
24
光明
14
9
5
23
远大
14
7
a
21
卫星
14
4
10
b
钢铁
14
0
14
14
…
…
…
…
…
A.负一场积1分,胜一场积2分B.卫星队总积分b=18
C.远大队负场数a=7D.某队的胜场总积分可以等于它的负场总积分
-
科目: 来源: 题型:
查看答案和解析>>【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
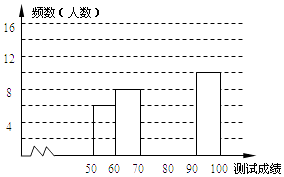
请结合图表完成下列各题:
(1)①表中a的值为 , 中位数在第组;
②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.组别
成绩x分
频数(人数)
第1组
50≤x<60
6
第2组
60≤x<70
8
第3组
70≤x<80
14
第4组
80≤x<90
a
第5组
90≤x<100
10
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题 1、如图1,线段AB的端点在正方形网格的格点上,在图1中找到格点C,使组成的△ABC的一个内角α满足tanα=2(找到两个点C,全等的三角形算一种)
2、
(1)如图1,线段AB的端点在正方形网格的格点上,在图1中找到格点C,使组成的△ABC的一个内角α满足tanα=2(找到两个点C,全等的三角形算一种).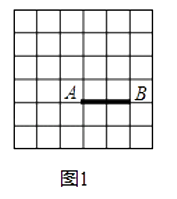
(2)如图2,在Rt△DEF中,∠DEF=90°,DE=1,sin∠F=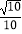 .用两块全等的△DEF拼出一个平行四边形,将拼得的平行四边形画在图2网格(网格图中小正方形边长均为1)中,画出不同的两种平行四边形(全等的算一种),并写出相应的周长.
.用两块全等的△DEF拼出一个平行四边形,将拼得的平行四边形画在图2网格(网格图中小正方形边长均为1)中,画出不同的两种平行四边形(全等的算一种),并写出相应的周长.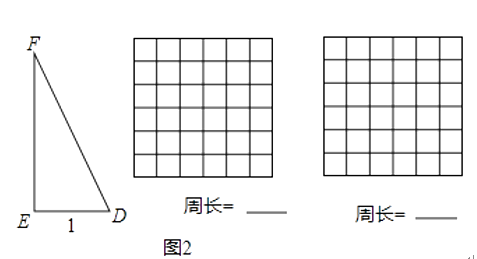
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,﹣3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1=
 ,直线AC解析式为y2=ax+b.
,直线AC解析式为y2=ax+b.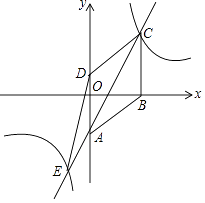
(1)求反比例函数解析式;
(2)当y1<y2时,求x的取值范围;
(3)求△CDE的面积.
相关试题

