【题目】以C为直角顶点的两个等腰直角△CAB和△CDG,E为AB的中点,F为DG的中点.
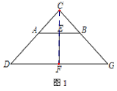
(1)如图1,点A、B分别在边CD,CG上,则EF与AD的数量关系是______________;
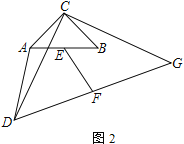
(2)如图2,点A、B不在边CD、CG上,(1)中EF与AD的关系还成立吗?请证明你的结论;
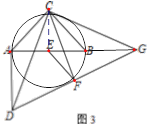
(3)如图3,若A、B、G在同一直线上,且A、C、B、F在同一圆上,直接写出△CDG与△CAB面积之比.


参考答案:
【答案】(1)AD=![]() EF;(2)成立,证明见解析;(3)
EF;(2)成立,证明见解析;(3)![]() .
.
【解析】试题分析:(1)连接CE、CF,证明C、E、F三点共线,然后在Rt△ACE中,由∠A=45°,可得AC=![]() CE,同理,DC=
CE,同理,DC=![]() CF,再根据AD=CD-AC,推导即可得;
CF,再根据AD=CD-AC,推导即可得;
(2)成立,连接CE、CF,通过证明△ACD∽△ECF,根据相似三角形对应边成比例即可得;
(3)连接CE,由A、C、B、F在同一圆上,可知点E为圆心,从而可得CE=EF,再由(2)AD=![]() EF、AC=
EF、AC=![]() CE从而可得AC=AD,由已知可得△ACD≌△BCG,从而可得∠ADC=∠AGB=22.5°,可得∠DAG=90°,设AE=x,则AB =2x,AG=2x+
CE从而可得AC=AD,由已知可得△ACD≌△BCG,从而可得∠ADC=∠AGB=22.5°,可得∠DAG=90°,设AE=x,则AB =2x,AG=2x+![]() x,AD=
x,AD=![]() x,由勾股定理DG2= (8+4
x,由勾股定理DG2= (8+4![]() )x2,再由△CDG∽△CAB,可得
)x2,再由△CDG∽△CAB,可得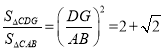 .
.
试题解析:(1)如图(1)连接CE,CF,
∵CA=CB,CD=CG,E为AB中点,F为DG中点,∴CE⊥AB,CF⊥DG,
∵∠C=90°,∴∠CAB=∠CDG=45°,∴AB//DG,∴C、E、F三点共线,
在Rt△ACE中,∠A=45°,∴AC=![]() CE,
CE,
同理,DC=![]() CF,
CF,
∵AD=CD-AC,EF=CF-CE,
∴AD=![]() EF,
EF,
故答案为:AD=![]() EF;
EF;
(2)成立.
连接CE、CF,
∵∠ACB=∠DCG=90°,CA=CB,CD=CG,AE=BE,DF=GF,
∴∠ACE=45°,∠DCF=45°,∠CAB=∠CDG=45°,∠AEC=∠DFC=90°,
∴∠ACD=∠ECF,
在Rt△ACE中,∠CAE=45°,∴AC=![]() CE,
CE,
同理,DC=![]() CF,
CF,
∴AC:CE=DC:CF,
∴△ACD∽△ECF,∴AD:EF=AC:CE=![]() ,
,
∴AD=![]() EF;
EF;
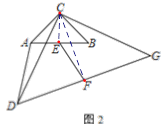
(3)连接CE,
∵A、C、B、F四点共圆,∠ACB=90°,AE=EB,∴E为圆心,
∴AE=CE=EF=BE,
∵∠ACB=∠DCG=90°,∴∠ACD=∠BCG,
∵AC=BC,DC=GC,∴△ACD≌△BCG,
∴BG=AD,∠CDA=∠CGB,
由(2)AD=![]() EF、AC=
EF、AC=![]() CE,∴AD=AC,
CE,∴AD=AC,
∴CB=BG,∴∠BCG=∠BGC,
∵∠BCG+∠BGC=∠ABC=45°,
∴∠BGC=22.5°,
∴∠ADC=22.5°,
∵∠CGD=∠CDG=45°,∴∠AGD=22.5°,
∴∠AGD+∠CDG+∠ADC=90°,
∴∠DAG=90°,
设AE=x,则AB =2x,AG=2x+![]() x,AD=
x,AD=![]() x,
x,
由勾股定理DG2=AD2+AG2,
∴DG2=(![]() x)2+(2x+
x)2+(2x+![]() x)2=(8+4
x)2=(8+4![]() )x2,
)x2,
∵△CDG∽△CAB,
∴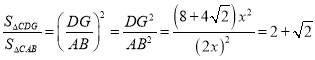 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某实验学校校友会在今年开学初,到新华书店采购文学名著和自然科学两类图书.经了解,购买30本文学名著和50本自然科学书共需2350元,20本文学名著比20本自然科学书贵500元.
(1)求每本文学名著和自然科学书的单价.
(2)若该校校友会要求购买自然科学书比文学名著多30本,总费用不超过2400元,请求出至多购买文学名著多少本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围
解:∵x﹣y=2,∴x=y+2.
又∵x>1,∴y+2>1.∴y>﹣1.
又∵y<0,∴﹣1<y<0. …①
同理得:1<x<2. …②
由①+②得﹣1+1<y+x<0+2
∴x+y的取值范围是0<x+y<2
请按照上述方法,完成下列问题:
已知关于x、y的方程组
 的解都为正数.
的解都为正数.(1)求a的取值范围;
(2)已知a﹣b=3,且b≤1,求a+b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工艺品每件的成本是50元,在某段时间内若以每件x元出售,可卖出(200-2x)件,设这段时间内售出该工艺品的利润为y元.
(1)直接写出利润y(元)与售价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果要使利润不低于1200元,且成本不超过2500元,请直接写出x的范围为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线y=
 x2—1与x轴交于A、B两点,顶点为C.
x2—1与x轴交于A、B两点,顶点为C.(1)求A,B两点的坐标;
(2)若点P为抛物线上的一点,且S△APC=2,求点P的坐标;
(3)如图2,P(﹣2,﹣2),直线BD交抛物线于D,交y轴于M,连DP交抛物线于E,连BE交y轴于N,求CM ON的值.

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=ax+b与二次函数y=ax2﹣b的图象可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】新合作超市最近进了一批玩具,进价每个15元,今天共卖山20个,实际卖出的价格以每个18元为标准,超过的记为正,不足的记为负,记录如下:
实际每个售出价格与标准的差值(单位:元)
+3
-1
+2
+1
个数
5
4
6
5
(1)这个超市今天卖出玩具的平均价格是多少?
(2)这个超市今天卖出的玩具赚了多少元?
相关试题

