Question

【题目】如图1，已知抛物线y=x2—1与x轴交于A、B两点，顶点为C．

（1）求A，B两点的坐标；

（2）若点P为抛物线上的一点，且S△APC=2，求点P的坐标；

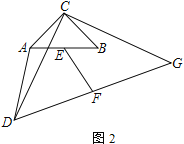
（3）如图2，P（﹣2，﹣2），直线BD交抛物线于D，交y轴于M，连DP交抛物线于E，连BE交y轴于N，求CM ON的值．

图1 图2

Answer 1

【答案】（1）A（﹣2，0），B（2，0）；（2）P（﹣4，3）或P（2，0）；（3）2．

【解析】试题分析：（1）令y=0，则有0=x2—1，解方程即可得；

（2）在y轴正半轴上取一点M使S△ACM=2，则可得M（0，1），过M作AC的平行线与抛物线的交点即为满足条件的点；

（3）根据已知设yDP=kx+2k－2，D（x1，y1），E（x2，y2），联立可得x1+x2=4k，x1·x2=4－8k，从而有，从而可得OM=，同理：ON=，继而可得OM·ON=．

试题解析：（1）令y=0，则有0=x2—1，解得：x1=-2，x2=2，∴A（﹣2，0），B（2，0）；

（2）由y=x2—1顶点为C，∴C（0，-1），

在y轴正半轴上取一点M使S△ACM=2，

∵A（-2，0），∴M（0，1），

∵A（-2，0），C（0，-1），

∴直线AC：y= ,

过M作AC的平行线MP，则直线MP：y= ，

解方程组 得: ，

∴P（﹣4，3）或P（2，0）；

（3）设yDP=kx+2k－2，D（x1，y1），E（x2，y2），

联立得x2－4kx－8k+4=0，∴x1+x2=4k，x1·x2=4－8k，

，

当x=0时，OM=，

同理：ON=，

所以OM·ON=．