【题目】如图,AB是⊙O的直径,AE交⊙O于点F,且与⊙O的切线CD互相垂直,垂足为D.
(1)求证:∠EAC=∠CAB;
(2)若CD=4,AD=8,求⊙O的半径.

参考答案:
【答案】(1)证明见解析;(2)⊙O的半径为5.
【解析】试题分析:(1)首先连接OC,由CD是 O的切线,CD⊥OC,又由CD⊥AE,即可判定OC∥AE,根据平行线的性质与等腰三角形的性质,即可证得∠EAC=∠CAB;
(2)连接BC,易证得△ACD∽△ABC,根据相似三角形的对应边成比例,即可求得AB的长,继而可得⊙O的半径长.
(1)证明:连接OC.
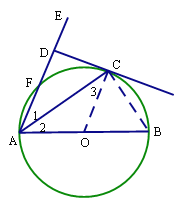
∵CD是⊙O的切线,
∴CD⊥OC,
又∵CD⊥AE,
∴OC∥AE,
∴∠1=∠3,
∵OC=OA,
∴∠2=∠3,
∴∠1=∠2,
即∠EAC=∠CAB;
(2)解:连接BC.
∵AB是⊙O的直径,CD⊥AE于点D,
∴∠ACB=∠ADC=90°,
∵∠1=∠2,
∴△ACD∽△ABC,
∴![]() ,
,
∵AC2=AD2+CD2=42+82=80,
∴AB=![]() =10,
=10,
∴⊙O的半径为10÷2=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
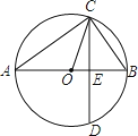
(1)求证:∠ACO=∠BCD;
(2)若BE=3,CD=8,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知正方形
 的顶点
的顶点 分别在
分别在 轴和
轴和 轴上,边
轴上,边 交
交 轴的正半轴于点
轴的正半轴于点 .
.

(1)若
 ,且
,且 ,求
,求 点的坐标;
点的坐标;(2)在(l)的条件下,若
 ,求
,求 点的坐标;
点的坐标;(3)如图2,连结
 交
交 轴于点
轴于点 ,点
,点 是
是 点上方
点上方 轴上一动点,以
轴上一动点,以 、
、 为边作
为边作 ,使
,使 点恰好落在
点恰好落在 边上,试探讨
边上,试探讨 ,
, 与
与 的数量关系,并证明你的结论.
的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄.
(1)设汽车行驶到公路AB上点P位置时,距离村庄M最近;行驶到点Q位置时,距离村庄N最近.请在图中的公路AB上分别画出点P,Q的位置(保留画图痕迹).
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离M,N两村庄都越来越近?在哪一段路上距离村庄N越来越近,而离村庄M却越来越远?(分别用文字表述你的结论,不必证明).
(3)到在公路AB上是否存在这样一点H,使汽车行驶到该点时,与村庄M,N的距离相等?如果存在,请在图中的AB上画出这一点(保留画图痕迹,不必证明);如果不存在,请简要说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知
 ,
, ,
, ,
, ,且以
,且以 为顶点的四边形为菱形.
为顶点的四边形为菱形.
(1)直接写出
 点的坐标;
点的坐标;(2)请用无刻度直尺作直线
 ,使直线
,使直线 经过点
经过点 且平分菱形的面积,保留作图痕迹(若无法打印答题卡,不便于规范作图,请用几何语言直接描述具体的作图过程代替作图);
且平分菱形的面积,保留作图痕迹(若无法打印答题卡,不便于规范作图,请用几何语言直接描述具体的作图过程代替作图);(3)已知点
 是
是 边上一点,若线段
边上一点,若线段 将菱形
将菱形 的面积分为
的面积分为 两部分,直接写出点
两部分,直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:
 ≈1.41,结果精确到0.1米)
≈1.41,结果精确到0.1米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.

相关试题

