【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.

参考答案:
【答案】(1)相切,理由见解析;(2)DE=![]() .
.
【解析】试题分析:(1)连接AD,OD,根据已知条件证得OD⊥DE即可;
(2)根据勾股定理计算即可.
解:(1)相切,
理由如下:
连接AD,OD,
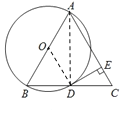
∵AB为⊙O的直径,
∴∠ADB=90°.
∴AD⊥BC.
∵AB=AC,
∴CD=BD=![]() BC.
BC.
∵OA=OB,
∴OD∥AC.
∴∠ODE=∠CED.
∵DE⊥AC,
∴∠ODE=∠CED=90°.
∴OD⊥DE.
∴DE与⊙O相切.
(2)由(1)知∠ADC=90°,
∴在Rt△ADC中,由勾股定理得,
AD=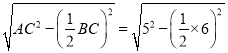 =4.
=4.
∵SACD=![]() ADCD=
ADCD=![]() ACDE,
ACDE,
∴![]() ×4×3=
×4×3=![]() ×5DE.
×5DE.
∴DE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AE交⊙O于点F,且与⊙O的切线CD互相垂直,垂足为D.
(1)求证:∠EAC=∠CAB;
(2)若CD=4,AD=8,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知
 ,
, ,
, ,
, ,且以
,且以 为顶点的四边形为菱形.
为顶点的四边形为菱形.
(1)直接写出
 点的坐标;
点的坐标;(2)请用无刻度直尺作直线
 ,使直线
,使直线 经过点
经过点 且平分菱形的面积,保留作图痕迹(若无法打印答题卡,不便于规范作图,请用几何语言直接描述具体的作图过程代替作图);
且平分菱形的面积,保留作图痕迹(若无法打印答题卡,不便于规范作图,请用几何语言直接描述具体的作图过程代替作图);(3)已知点
 是
是 边上一点,若线段
边上一点,若线段 将菱形
将菱形 的面积分为
的面积分为 两部分,直接写出点
两部分,直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:
 ≈1.41,结果精确到0.1米)
≈1.41,结果精确到0.1米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 ,
, ,
, ,
, 分别是四边形
分别是四边形 各边的中点,且
各边的中点,且 ,
, ,
, .
.
(1)试判断四边形
 的形状,并证明你的结论;
的形状,并证明你的结论;(2)如图2,依次取
 ,
, ,
, ,
, 的中点
的中点 ,
, ,
, ,
, ,再依次取
,再依次取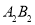 ,
, ,
, ,
, 的中点
的中点 ,
, ,
, ,
, ……以此类推,取
……以此类推,取 ,
, ,
,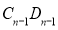 ,
, 的中点
的中点 ,
, ,
, ,
, ,根据信息填空:
,根据信息填空:①四边形
 的面积是__________;
的面积是__________;②若四边形
 的面积为
的面积为 ,则
,则 ________;
________;③试用
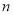 表示四边形
表示四边形 的面积___________.
的面积___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使50%左右的人获得折扣优惠.某市针对乘坐地铁的人群进行了调查.调查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.下列说法正确的是( )

①每人乘坐地铁的月均花费最集中的区域在80~100元范围内;
②每人乘坐地铁的月均花费的平均数范围是40~60元范围内;
③每人乘坐地铁的月均花费的中位数在60~100元范围内;
④乘坐地铁的月均花费达到80元以上的人可以享受折扣.
A.①②④B.①③④C.③④D.①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 经过第一、二、三象限,与
经过第一、二、三象限,与 轴交于点
轴交于点 ,点
,点 在这条直线上,连接
在这条直线上,连接 ,已知
,已知 的面积等于1.
的面积等于1.
(1)求
 的值;
的值;(2)如果反比例函数y=
 (k是常量,k≠0)的图象经过点A,求这个反比例函数的解析式。
(k是常量,k≠0)的图象经过点A,求这个反比例函数的解析式。
相关试题

