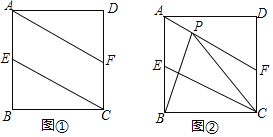
【题目】如图![]() ,矩形ABCD中,
,矩形ABCD中,![]() ,
,![]() ,E、F分别是AB、CD的中点
,E、F分别是AB、CD的中点
![]() 求证:四边形AECF是平行四边形;
求证:四边形AECF是平行四边形;
![]() 是否存在a的值使得四边形AECF为菱形,若存在求出a的值,若不存在说明理由;
是否存在a的值使得四边形AECF为菱形,若存在求出a的值,若不存在说明理由;
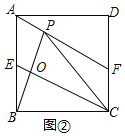
![]() 如图
如图![]() ,点P是线段AF上一动点且
,点P是线段AF上一动点且![]()
![]() 求证:
求证:![]() ;
;
![]() 直接写出a的取值范围.
直接写出a的取值范围.
参考答案:
【答案】(1)证明见解析;(2)不存在;(3)①证明见解析;②![]() .
.
【解析】
(1)由矩形性质得![]() ,
,![]() ,再证
,再证![]() 且
且![]() 即可;(2)不存在,由
即可;(2)不存在,由![]() 知:当
知:当![]() 时,四边形AECF为菱形,可得
时,四边形AECF为菱形,可得![]() ,此方程无解;(3)由平行线性质得
,此方程无解;(3)由平行线性质得![]() ,证得
,证得![]() ,
,![]() ,由
,由![]() ,
,![]() ,得OE是三角形的中位线,所以
,得OE是三角形的中位线,所以![]() ,根据中垂线性质得
,根据中垂线性质得![]() ;如图
;如图![]() 当P与F重合时,
当P与F重合时,![]() ,
,![]() 的取值范围是
的取值范围是![]() .
.
![]() 证明:
证明:![]() 四边形ABCD是矩形,
四边形ABCD是矩形,
![]() ,
,![]() ,
,
又![]() 、F分别是边AB、CD的中点,
、F分别是边AB、CD的中点,
![]() ,
,
![]() 四边形AECF是平行四边形;
四边形AECF是平行四边形;
![]() 解:不存在,
解:不存在,
由![]() 知:四边形AECF是平行四边形;
知:四边形AECF是平行四边形;
当![]() 时,四边形AECF为菱形,
时,四边形AECF为菱形,
![]() 四边形ABCD是矩形,
四边形ABCD是矩形,
![]() ,
,
![]() ,
,![]()
![]() ,
,
方程无解,故不存在这样的a;
![]() 解:
解:![]() 如图
如图![]() ,
,
![]() 四边形AECF是平行四边形,
四边形AECF是平行四边形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 如图
如图![]() ,当P与F重合时,
,当P与F重合时,![]() ,
,
![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定运算符号的意义是:当a>b时,ab=a﹣b;当a<b时,ab=a+b.
(1)计算:61= ;(﹣3)2= ;
(2)棍据运算符号的意义且其他运算符号意义不变的条件下,
①计算:﹣14+15×[(﹣
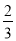 )(﹣
)(﹣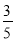 )]﹣(3223)÷(﹣7),
)]﹣(3223)÷(﹣7),②若x,y在数轴上的位置如图所示,
a.填空:x2+1 y(填“>“或“<”):
b.化简:[(x2+x+1)(x+y)]+[(y﹣x2)(y+2)].

-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步提升企业产品竞争力,某企业加大了科研经费的投入,2016年该企业投入科研经费5000万元,2018年投入科研经费7200万元,假设该企业这两年投入科研经费的年平均增长率相同.
 求这两年该企业投入科研经费的年平均增长率.
求这两年该企业投入科研经费的年平均增长率. 若该企业科研经费的投入还将保持相同的年平均增长率,请你预算2020年该企业投入科研经费多少万元.
若该企业科研经费的投入还将保持相同的年平均增长率,请你预算2020年该企业投入科研经费多少万元. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了对学生进行多元化的评价,某中学决定对学生进行综合素质评价
 设该校中学生综合素质评价成绩为x分,满分为100分评价等级与评价成绩x分之间的关系如下表:
设该校中学生综合素质评价成绩为x分,满分为100分评价等级与评价成绩x分之间的关系如下表:中学生综合素质评价成绩
中学生综合素质评价等级

A级

B级

C级

D级
现随机抽取该校部分学生的综合素质评价成绩,整理绘制成图
 、图
、图 两幅不完整的统计图
两幅不完整的统计图 请根据相关信息,解答下列问题:
请根据相关信息,解答下列问题:(1)在这次调查中,一共抽取了______名学生,图
 中等级为D级的扇形的圆心角
中等级为D级的扇形的圆心角 等于______
等于______ ;
;(2)补全图
 中的条形统计图;
中的条形统计图;(3)若该校共有1200名学生,请你估计该校等级为C级的学生约有多少名.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内,分别用3根、5根、6根……火柴棒首尾依次相接,能搭成什么形状的三角形呢?通过尝试,列表如下.
火柴棒数
3
5
6
…
示意图
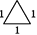
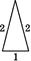
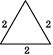
…
形状
等边三角形
等腰三角形
等边三角形
…
问:(1)4根火柴棒能搭成三角形吗?
(2)8根、12根火柴棒分别能搭成几种不同形状的三角形?并画出它们的示意图.
-
科目: 来源: 题型:
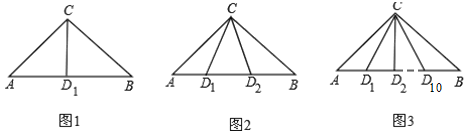
查看答案和解析>>【题目】(1)如图1,D1是△ABC的边AB上的一点,则图中有哪几个三角形?
(2)如图2,D1,D2是△ABC的边AB上的两点,则图中有哪几个三角形?
(3)如图3,D1,D2,…,D10是△ABC的边AB上的10个点,则图中共有多少个三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点P(2,
 )绕原点O顺时针旋转90°后得到点P′,则点P′的坐标是( )
)绕原点O顺时针旋转90°后得到点P′,则点P′的坐标是( )A. (-2,
 ) B. (
) B. ( ,2) C. (2,-
,2) C. (2,- ) D. (
) D. ( ,-2)
,-2)
相关试题

