【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,则OC= 
参考答案:
【答案】![]()
【解析】解:∵正方形ABCD中,AB=BC=CD=4,∠B=∠DCF,
又∵AE=BF,
∴BE=CF=4﹣1=3,DF= ![]() =
= ![]() =5,
=5,
则在直角△BEC和直角△CFD中, ,
,
∴△BEC≌△CFD,
∴∠BEC=∠CFD,
又∵直角△BCE中,∠BEC+∠BCE=90°,
∴∠CFD+∠BCE=90°,
∴∠FOC=90°,即OC⊥DF,
∴S△CDF= ![]() CDCF=
CDCF= ![]() OCDF,
OCDF,
∴OC= ![]() =
= ![]() =
= ![]() .
.
故答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用正方形的性质和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗共17棵.若购进1棵A种树苗与2棵B种树苗共需200元;购进2棵A种树苗与1棵B种树苗共需220元.
(1)求购进A种树苗和B种树苗每棵各多少元?
(2)若小区购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?
(3)若购进B种树苗的数量少于A种树苗的数量,请设计一种费用最省的方案,并求出该方案所需费用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,下列说法不正确的是( )

A. 汽车在行驶途中停留了0.5小时
B. 汽车在行驶途中的平均速度为
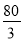 千米/小时
千米/小时C. 汽车共行驶了240千米
D. 汽车自出发后3小时至4.5小时之间行驶的速度是80千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“南山”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班组织去方特参加秋季社会实践活动,其中第一小组有x人,第二小组的人数比第一小组人数的
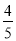 少30人,如果从第二小组调出10人到第一小组,那么:
少30人,如果从第二小组调出10人到第一小组,那么:(1)两个小组共有多少人?
(2)调动后,第一小组的人数比第二小组多多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
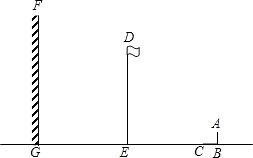
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.
相关试题

