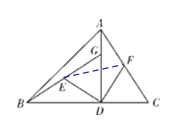
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由已知条件先证△BDG≌△ADC,再证△BDE≌△ADF即可得到所求结论;
(2)如图,由(1)可知∠ADC=90°,△DEF是等腰直角三角形, 结合F是AC的中点可得DF=![]() AC=5,这样用勾股定理即可求得EF的长度.
AC=5,这样用勾股定理即可求得EF的长度.
试题解析:
(1)∵AD⊥BC于点D,
∴∠BDG=∠ADC=90°.
∵BD=AD,DG=DC,
∴△BDG≌△ADC,
∴BG=AC.
∵E,F分别是BG,AC的中点,
∴DE=![]() BG,DF=
BG,DF=![]() AC.
AC.
∴DE=DF.
又∵BD=AD,BE=AF,
∴△BDE≌△ADF.
∴∠BDE=∠ADF.
∴∠EDF=∠EDG+∠ADF=∠EDG+∠BDE=∠BDG=90°.
∴DE⊥DF.
(2)如图,连接EF,
∵AC=10,∠ADC=90°,
∴DE=DF=![]() AC=5.
AC=5.
又∵∠EDF=90°,
∴EF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 中,
中, ,把
,把 绕A点沿顺时针方向旋转得到
绕A点沿顺时针方向旋转得到 ,连接BD,CE交于点F.
,连接BD,CE交于点F.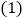 求证:
求证: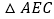 ≌
≌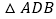 ;
; 若
若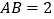 ,
,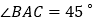 ,当四边形ADFC是菱形时,求BF的长.
,当四边形ADFC是菱形时,求BF的长.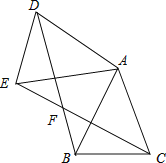
-
科目: 来源: 题型:
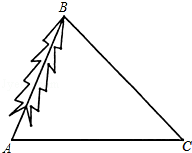
查看答案和解析>>【题目】为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=21m,∠BAC=53°,求这颗古杉树AB的长度. (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,点P是CD边上一动点,连接PA,分别过点B、D作
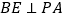 、
、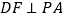 ,垂足分别为E、F.
,垂足分别为E、F.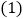 如图
如图 ,请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?
,请探究BE、DF、EF这三条线段的长度具有怎样的数量关系?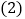 若点P在DC的延长线上,如图
若点P在DC的延长线上,如图 ,那么这三条线段的长度之间又具有怎样的数量关系?
,那么这三条线段的长度之间又具有怎样的数量关系?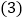 若点P在CD的延长线上,如图
若点P在CD的延长线上,如图 ,请直接写出结论.
,请直接写出结论.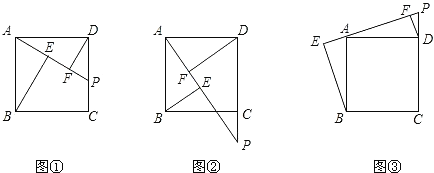
-
科目: 来源: 题型:
查看答案和解析>>【题目】将背面相同,正面分别标有数字1,2,3,4的四张卡片洗匀后,背面朝上放在桌面上.
(1)从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率;
(2)先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明. -
科目: 来源: 题型:
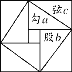
查看答案和解析>>【题目】我们运用图(Ⅰ)中大正方形的面积可表示为(a+b)2,也可表示为c3+4(
 ab),即(a+b)2=c2+4(
ab),即(a+b)2=c2+4( ab)由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab)由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.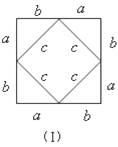
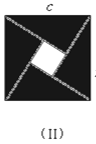
(1)请你用图(Ⅱ)(2002年国际数学家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a,较小的直角边长都为b,斜边长都为c).
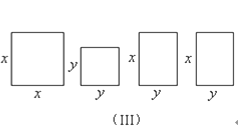
(2)请你用(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+2y)2=x2+4xy+4y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(图1),后人称其为“赵爽弦图”,由弦图变化得到图2,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=12,则S2的值为_______.
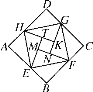
(图1) (图2)
相关试题

