【题目】在学校组织的“学习强国”知识竞赛中,每班参加比赛的人数相同,成绩分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级其中相应等级的得分依次记为
四个等级其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分和
分和![]() 分.年级组长张老师将
分.年级组长张老师将![]() 班和
班和![]() 班的成绩进行整理并绘制成如下的统计图:
班的成绩进行整理并绘制成如下的统计图:
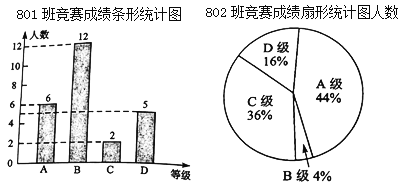
(1)在本次竞赛中,![]() 班
班![]() 级的人数有多少。
级的人数有多少。
(2)请你将下面的表格补充完整:
成绩 班级 | 平均数(分) | 中位数 (分) | 众数 (分) | B级及以上人数 |
|
|
|
| |
|
|
|
(3)结合以上统计量,请你从不同角度对这次竞赛成绩的结果进行分析(写出两条)
参考答案:
【答案】(1)9人;(2)见解析;(3)略.
【解析】
(1)根据一班的成绩统计可知一共有25人,因为每班参加比赛的人数相同,用总人数乘以C级以上的百分比即可得出答案,
(2)根据平均数、众数、中位数的概念,结合一共有25人,即可得出答案.
(3)分别从![]() 级及以上人数和众数的角度分析那个班成绩最好即可.
级及以上人数和众数的角度分析那个班成绩最好即可.
解:(1)![]() 班有
班有![]() 人,
人,![]() 人.
人.
所以![]() 班C级人数有9人
班C级人数有9人
(2)请你将下面的表格补充完整:
平均数(分) | 中位数(分) | 众数(分) |
| |
| 87.6 | 90 |
| 18 |
| 87.6 |
| 100 |
|
(3)从![]() 级及以上人数条看,
级及以上人数条看,![]() 班的人数多于
班的人数多于![]() 班人数,此时
班人数,此时![]() 班的成绩好些
班的成绩好些
从众数的角度看,![]() 班的众数高于
班的众数高于![]() 班众数,此时802班的成绩差一些.
班众数,此时802班的成绩差一些.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果m<n<0,那么下列式子中错误的是( )
A. m-9<n-9 B. -m>-n C.
 <
<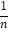 D.
D. 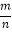 >1
>1 -
科目: 来源: 题型:
查看答案和解析>>【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”.
(提出问题)三个有理数a、b、c满足abc>0,求
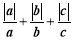 的值.
的值.(解决问题)由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c都是正数,即a>0,b>0,c>0时,
则:
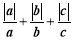 =
=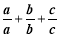 =1+1+1=3;
=1+1+1=3;②当a,b,c有一个为正数,另两个为负数时,设a>0,b<0,c<0,
即:
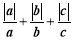 =
=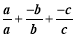 =1+(1)+(1)=1,所以
=1+(1)+(1)=1,所以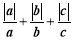 的值为3或1.
的值为3或1.(探究)请根据上面的解题思路解答下面的问题:
(1)已知a<0,b>0,c>0,则
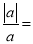 ,
,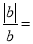 ,
,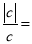 ;
;(2)三个有理数a,b,c满足abc<0,求
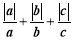 的值;
的值;(3)已知|a|=3,|b|=1,且a<b,求a+b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形ABCD折叠,使得对角线的两个端点A. C重合,折痕所在直线交直线AB于点E,如果AB=4,BE=1,则BC的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=﹣
 图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )A.x1<x2<x3 B.x1<x3<x2
C.x2<x1<x3 D.x2<x3<x1
-
科目: 来源: 题型:
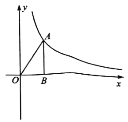
查看答案和解析>>【题目】如图,已知点
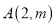 是反比例函数
是反比例函数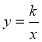
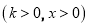 的图象上一点过点
的图象上一点过点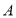 作
作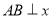 轴于点
轴于点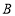 ,连结
,连结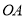 ,
,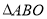 的面积为
的面积为 .
.
(1)求
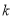 和
和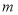 的值.
的值.(2)直线
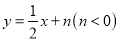 与
与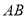 的延长线交于点
的延长线交于点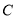 ,与反比例函数图象交于点
,与反比例函数图象交于点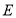 .
.①若
 ,求点
,求点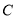 坐标;②若点
坐标;②若点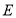 到直线
到直线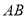 的距离等于
的距离等于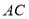 ,求
,求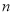 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形的边长为4,甲、乙两动点分别从正方形
 的顶点
的顶点 同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若乙的速度是甲的速度的3倍,则它们第2 019次相遇在( )
同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若乙的速度是甲的速度的3倍,则它们第2 019次相遇在( )
A.
 边上 B.
边上 B.  边上 C.
边上 C.  边上 D.
边上 D.  边上
边上
相关试题

