【题目】某天,一蔬菜经营户用120元钱按批发价从蔬菜批发市场买了西红柿和豆角共40kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 2.4 | 3.2 |
零售价(单位:元/kg) | 3.8 | 5.2 |
如果西红柿和豆角全部以零售价售出,他当天卖这些西红柿和豆角赚了多少元钱?
参考答案:
【答案】当天卖这些西红柿和豆角赚了74元钱.
【解析】试题分析:
设西红柿买了xkg,豆角买了ykg,根据总共用了120元买了两种蔬菜40kg列出方程组,解方程组求得x、y的值即可根据表中提供的信息求出当天所赚的钱是多少了.
试题解析:
设西红柿买了xkg,豆角买了ykg,根据题意得:
![]() ,解得:
,解得: ![]() ,
,
∴当天卖出这些蔬菜后赚的钱=10×(3.8-2.4)+30×(5.2-3.2)=14+60=74(元),
答:他当天卖出这些西红柿和豆角赚了74元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【回顾】
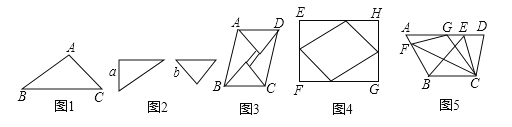
如图1,△ABC中,∠B=30°,AB=3,BC=4,则△ABC的面积等于 .
【探究】
图2是同学们熟悉的一副三角尺,一个含有30°的角,较短的直角边长为a;另一个含有45°的角,直角边长为b,小明用两副这样的三角尺拼成一个平行四边形ABCD(如图3),用了两种不同的方法计算它的面积,从而推出sin75°=
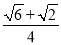 ,小丽用两副这样的三角尺拼成了一个矩形EFGH(如图4),也推出sin75°=
,小丽用两副这样的三角尺拼成了一个矩形EFGH(如图4),也推出sin75°= ,请你写出小明或小丽推出sin75°=
,请你写出小明或小丽推出sin75°=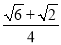 的具体说理过程.
的具体说理过程.【应用】
在四边形ABCD中,AD∥BC,∠D=75°,BC=6,CD=5,AD=10(如图5).
(1)点E在AD上,设t=BE+CE,求t2的最小值;
(2)点F在AB上,将△BCF沿CF翻折,点B落在AD上的点G处,点G是AD的中点吗?说明理由.
-
科目: 来源: 题型:
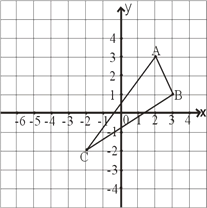
查看答案和解析>>【题目】如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).
(1)请在图中作出△ABC关于y轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直写出D、E、F的坐标.D、E、F点的坐标是:D( , ) E( , ) F( , );
(2)求四边形ABED的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,Rt△ACB 中,∠C=90°,点D在AC上,∠CBD=∠A,过A、D两点的圆的圆心O在AB上.
(1)利用直尺和圆规在图1中画出⊙O(不写作法,保留作图痕迹,并用黑色水笔把线条描清楚);
(2)判断BD所在直线与(1)中所作的⊙O的位置关系,并证明你的结论;
(3)设⊙O交AB于点E,连接DE,过点E作EF⊥BC,F为垂足,若点D是线段AC的黄金分割点(即
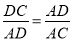 ),如图2,试说明四边形DEFC是正方形.
),如图2,试说明四边形DEFC是正方形.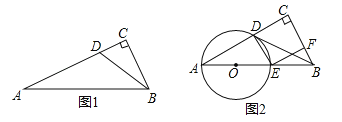
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解射击运动员小杰的集训效果,教练统计了他集训前后的两次测试成绩(每次测试射击10次),制作了如图所示的条形统计图.
(1)集训前小杰射击成绩的众数为 ;
(2)分别计算小杰集训前后射击的平均成绩;
(3)请用一句话评价小杰这次集训的效果.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴上,点B坐标为(4,t)(t>0),二次函数
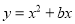 (b<0)的图象经过点B,顶点为点D.
(b<0)的图象经过点B,顶点为点D.(1)当t=12时,顶点D到x轴的距离等于 ;
(2)点E是二次函数
 (b<0)的图象与x轴的一个公共点(点E与点O不重合),求OEEA的最大值及取得最大值时的二次函数表达式;
(b<0)的图象与x轴的一个公共点(点E与点O不重合),求OEEA的最大值及取得最大值时的二次函数表达式;(3)矩形OABC的对角线OB、AC交于点F,直线l平行于x轴,交二次函数
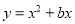 (b<0)的图象于点M、N,连接DM、DN,当△DMN≌△FOC时,求t的值.
(b<0)的图象于点M、N,连接DM、DN,当△DMN≌△FOC时,求t的值.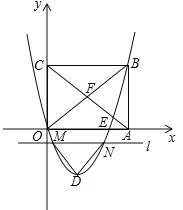
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,0)和B(0,b)满足
 ,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,描出此时P点的位置,并写出点P的位置坐标;
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B′P′,若B′P′将四边形OACB的周长分成相等的两部分,求h的值.

相关试题

