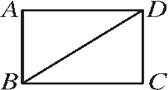
【题目】如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD,BC于点E,F,垂足为点O;(要求用尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)中,连接BE和DF,求证:四边形DEBF是菱形
参考答案:
【答案】(1)作图见解析;(2)证明见解析.
【解析】(1)分别以B、D为圆心,以大于![]() 的长为半径四弧交于两点,过两点作直线即可得到线段BD的垂直平分线;(2)利用垂直平分线证得△DEO≌△BFO即可证得EO=FO,进而利用菱形的判定方法得出结论.
的长为半径四弧交于两点,过两点作直线即可得到线段BD的垂直平分线;(2)利用垂直平分线证得△DEO≌△BFO即可证得EO=FO,进而利用菱形的判定方法得出结论.
本题解析: (1)如图所示:EF即为所求;

(2)证明:如图所示:∵四边形ABCD为矩形,∴AD∥BC,∴∠ADB=∠CBD,
∵EF垂直平分线段BD,∴BO=DO,
在△DEO和三角形BFO中,
∵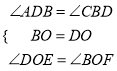
∴△DEO≌△BFO(ASA),∴EO=FO,
∴四边形DEBF是平行四边形,又∵EF⊥BD,
∴四边形DEBF是菱形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】央视举办的《中国诗词大会》受到广大的关注.深圳某中学学生会就《中国诗词大会》节目的喜爱程度,在校内进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D;根据调查结果绘制出如图所示的扇形和条形统计图,请结合图中所给信息解答下列问题:

(1)本次被调查的对象共有 人;被调查者“不太喜欢”有 人;
(2)将扇形统计图和条形统计图补充完整;
(3)假设这所学校有1500名学生,请据此估计“比较喜欢”的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料:
按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为a1,排在第二位的数称为第二项,记为a2,以此类推,排在第n位的数称为第n项,记为
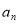 .所以,数列的一般形式可以写成:
.所以,数列的一般形式可以写成: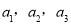 ,…,
,…,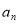 ,…,一般的,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,期中a1=1,a2=3,公差为d=2.根据以上材料,解答下列问题:
,…,一般的,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,期中a1=1,a2=3,公差为d=2.根据以上材料,解答下列问题:(1)等差数列5,10,15,…的公差d为 ,第5项是 .
(2)如果一个数列
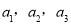 ,…,
,…,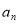 ,…,是等差数列,且公差为d,那么根据定义可得到:
,…,是等差数列,且公差为d,那么根据定义可得到: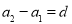 ,
,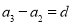 ,
,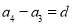 ,…,
,…,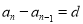 ,….所以
,….所以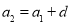
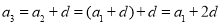
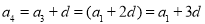
……由此,请你填空完成等差数列的通项公式:
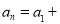 ( )d
( )d(3)求-4039是等差数列-5,-7,-9,…的第几项?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=
 BD
BD其中正确结论的为______(请将所有正确的序号都填上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD//BC,
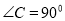 ,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).(1)设
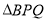 的面积为
的面积为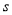 ,直接写出
,直接写出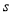 与
与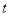 之间的函数关系式是____________(不写取值范围).
之间的函数关系式是____________(不写取值范围).(2)当B,P,Q三点为顶点的三角形是等腰三角形时,求出此时
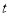 的值.
的值.(3)当线段PQ与线段AB相交于点O,且2OA=OB时,直接写出
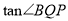 =_____________.
=_____________.(4)是否存在时刻
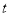 ,使得
,使得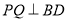 若存在,求出
若存在,求出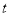 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.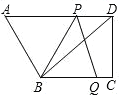
-
科目: 来源: 题型:
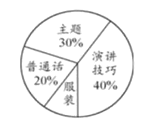
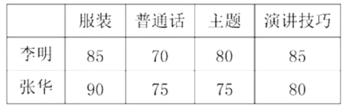
查看答案和解析>>【题目】某校为选拔一名选手参加“美丽江门,我为侨乡做代言”主题演讲比赛,经研究,按下图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
结合以上信息,回答下列问题:
(1)求服装项目在选手考评中的权数;
(2)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽江门,我为侨乡做代言”主题演讲比赛,并说明理由.
-
科目: 来源: 题型:
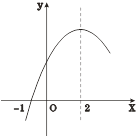
查看答案和解析>>【题目】二次函数
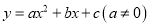 的部分图象如图③所示,图象过点(-1,0),对称轴为直线
的部分图象如图③所示,图象过点(-1,0),对称轴为直线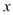 =2,则下列结论中正确的个数有( )
=2,则下列结论中正确的个数有( )①4
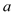 +b=0;②
+b=0;②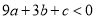 ;③若点A(-3,
;③若点A(-3, 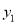 ),点B(-
),点B(-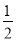 ,
, 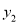 ),点C(5,
),点C(5, 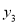 )在该函数图象上,则
)在该函数图象上,则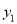 <
<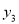 <
<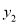 ;④若方程
;④若方程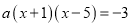 的两根为
的两根为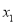 和
和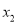 ,且
,且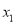 <
<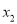 ,则
,则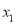 <-1<5<
<-1<5<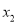 .
. 
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

