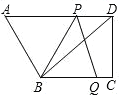
【题目】如图,在四边形ABCD中,AD//BC, ![]() ,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 与
与![]() 之间的函数关系式是____________(不写取值范围).
之间的函数关系式是____________(不写取值范围).
(2)当B,P,Q三点为顶点的三角形是等腰三角形时,求出此时![]() 的值.
的值.
(3)当线段PQ与线段AB相交于点O,且2OA=OB时,直接写出![]() =_____________.
=_____________.
(4)是否存在时刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,
, ![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】试题分析:
(1)由题意可得BQ=BC-CQ=4-t,点P到BC的距离=CD=3,由此结合三角形的面积公式即可得到S与t之间的函数关系式;
(2)过点P作PH⊥BC于点H,结合勾股定理和已知条件把BP2、BQ2、PQ2用含“t”的代数式表达出来,然后分BP=BQ、BP=PQ、BQ=PQ三种情况列出方程,解方程得到对应的t的值,再结合题中的条件检验即可得到符合要求的t的值;
(3)如图2,过点P作PM⊥BC交CB的延长线于点M,易证得四边形PMCD是矩形,由此可得PM=CD=3,CM=PD=2t,结合AD=6,BC=4,可得PA=2t-6,BQ=4-t,MQ=CM-CQ=t,由AD∥BC可得△OAP∽△OBQ,结合2OA=OB即可求得t的值,从而可由tan∠BQP=![]() 求得其值;
求得其值;
(4)如图3,过点D作DM∥PQ交BC的延长线于点M,则当∠BDM=90°时,PQ⊥BD,即当BM2=DM2+BD2时,PQ⊥BD,由此结合已知条件把DM2、BM2和BD2用含“t”的式子表达出来,列出方程就可得解得t的值.
试题解析:
(1)由题意可得BQ=BC-CQ=4-t,点P到BC的距离=CD=3,
∴S△PBQ=![]() BQ×3=
BQ×3=![]() ;
;
(2)如下图,过点P作PH⊥BC于点H,
∴∠PHB=∠PHQ=90°,
∵∠C=90°,AD∥BC,
∴∠CDP=90°,
∴四边形PHCD是矩形,
∴PH=CD=3,HC=PD=2t,
∵CQ=t,BC=4,
∴HQ=CH-CQ=t,BH=BC-CH=4-2t,BQ=4-t,
∴BQ2=![]() ,BP2=
,BP2=![]() ,PQ2=
,PQ2=![]() ,
,
由BQ2=BP2可得: ![]() ,解得:无解;
,解得:无解;
由BQ2=PQ2可得: ![]() ,解得:
,解得: ![]() ;
;
由BP2= PQ2可得: ![]()
![]() ,解得:
,解得: ![]() 或
或![]() ,
,
∵当![]() 时,BQ=4-4=0,不符合题意,
时,BQ=4-4=0,不符合题意,
∴综上所述, ![]() 或
或![]() ;
;

(3)如图2,过点P作PM⊥BC交CB的延长线于点M,
∴∠PMC=∠C=90°,
∵AD∥BC,
∴∠D=90°,△OAP∽△OBQ,
∴四边形PMCD是矩形, ![]() ,
,
∴PM=CD=3,CM=PD=2t,
∵AD=6,BC=4,CQ=t,
∴PA=2t-6,BQ=4-t,MQ=CM-CQ=2t-t=t,
∴![]() ,解得:
,解得: ![]() ,
,
∴MQ= ![]() ,
,
又∵PM=3,∠PMQ=90°,
∴tan∠BPQ=![]() ;
;

(4)如图3,过点D作DM∥PQ交BC的延长线于点M,则当∠BDM=90°时,PQ⊥BD,即当BM2=DM2+BD2时,PQ⊥BD,
∵AD∥BC,DM∥PQ,
∴四边形PQMD是平行四边形,
∴QM=PD=2t,
∵QC=t,
∴CM=QM-QC=t,
∵∠BCD=∠MCD=90°,
∴BD2=BC2+DC2=25,DM2=DC2+CM2=9+t2,
∵BM2=(BC+CM)2=(4+t)2,
∴由BM2=BD2+DM2可得: ![]() ,解得:
,解得: ![]() ,
,
∴当![]() 时,∠BDM=90°,
时,∠BDM=90°,
即当![]() 时,PQ⊥BD.
时,PQ⊥BD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料:
按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为a1,排在第二位的数称为第二项,记为a2,以此类推,排在第n位的数称为第n项,记为
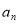 .所以,数列的一般形式可以写成:
.所以,数列的一般形式可以写成: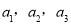 ,…,
,…,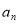 ,…,一般的,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,期中a1=1,a2=3,公差为d=2.根据以上材料,解答下列问题:
,…,一般的,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,期中a1=1,a2=3,公差为d=2.根据以上材料,解答下列问题:(1)等差数列5,10,15,…的公差d为 ,第5项是 .
(2)如果一个数列
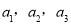 ,…,
,…,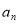 ,…,是等差数列,且公差为d,那么根据定义可得到:
,…,是等差数列,且公差为d,那么根据定义可得到: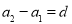 ,
,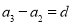 ,
,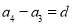 ,…,
,…,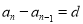 ,….所以
,….所以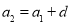
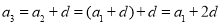
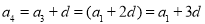
……由此,请你填空完成等差数列的通项公式:
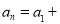 ( )d
( )d(3)求-4039是等差数列-5,-7,-9,…的第几项?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=
 BD
BD其中正确结论的为______(请将所有正确的序号都填上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD,BC于点E,F,垂足为点O;(要求用尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)中,连接BE和DF,求证:四边形DEBF是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为选拔一名选手参加“美丽江门,我为侨乡做代言”主题演讲比赛,经研究,按下图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
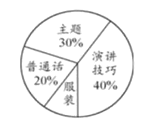
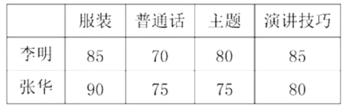
结合以上信息,回答下列问题:
(1)求服装项目在选手考评中的权数;
(2)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽江门,我为侨乡做代言”主题演讲比赛,并说明理由.
-
科目: 来源: 题型:
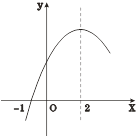
查看答案和解析>>【题目】二次函数
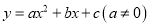 的部分图象如图③所示,图象过点(-1,0),对称轴为直线
的部分图象如图③所示,图象过点(-1,0),对称轴为直线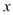 =2,则下列结论中正确的个数有( )
=2,则下列结论中正确的个数有( )①4
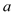 +b=0;②
+b=0;②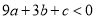 ;③若点A(-3,
;③若点A(-3, 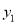 ),点B(-
),点B(-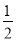 ,
, 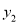 ),点C(5,
),点C(5, 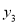 )在该函数图象上,则
)在该函数图象上,则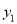 <
<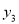 <
<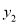 ;④若方程
;④若方程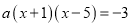 的两根为
的两根为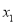 和
和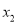 ,且
,且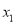 <
<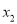 ,则
,则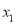 <-1<5<
<-1<5<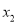 .
. 
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象与反比例函数
的图象与反比例函数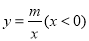 的图象交于A(-1,3),B(-3,n)两点,直线
的图象交于A(-1,3),B(-3,n)两点,直线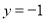 与
与 轴交于点C.
轴交于点C.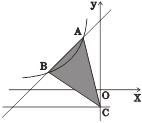
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
相关试题

