【题目】在△ABC 中,∠ACB=90° AD 是它的角平分线,EB⊥AB 于点 B 且交 AD 的延长线于点 E.
(1)如图 1,求证:BD=BE
(2)如图 2,过点 E 作 EF⊥BC 于点 F, CF:BF=5:3, BE=10,求 DF 的长.
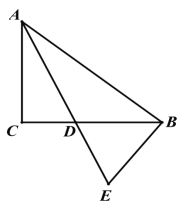
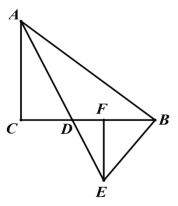
图 1 图 2
参考答案:
【答案】(1)证明见解析.(2)DF=4
【解析】分析: (1)过点B作BG⊥DE于G, 根据AD是△ABC的角平分线, EB⊥AB得∠ADC=∠E, 再证∠BGD=∠BGE,最后根据BG=BG可证△BDG≌△BEG,从而可得BD=BE.
(2)过点D作DH⊥AB于H,先证△BHD≌△EBF,得到 DH=BF,从而CD=BF.设CF=5x,BF=3x,根据BD=BF+DF可求出x的值,可求出DF的值.
详解:
(1)证明:过点B作BG⊥DE于G
∵AD是△ABC的角平分线
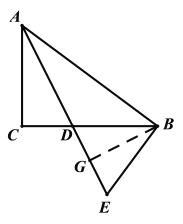
∴∠BAD=∠CAD
∵EB⊥AB
∴∠ABE=90°
在Rt△ABE中
∠BAE+∠E=90°
在Rt△ACD中
∠CAD+∠ADC=90°
∴∠ADC=∠E
∵∠ADC=∠BDE
∴∠BDE=∠E
∵BG⊥DE
∴∠BGD=∠BGE
∵BG=BG
∴△BDG≌△BEG(AAS)
∴BD=BE
(2)过点D作DH⊥AB于H,
∵ ∠ACB=90°
∴ CD⊥AC
∴ CD=DH
∵ ∠ABE=90°
∴ ∠ABC+∠FBE=90
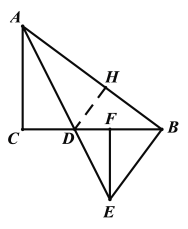
∵ EF⊥BD
∴ ∠BFE=90°
∴ ∠FEB+∠FBE=90°
∴ ∠HBD=∠FEB
∵ DH⊥AB
∴ ∠BHD=90°
∴ △BHD≌△EBF(AAS)
∴ DH=BF
∴ CD=BF
∵ CF:BF=5:3
∵ 设CF=5x,BF=3x,则CD=3x,
DF=CF-CD=5x-3x=2x
BD=BF+DF=3x+2x==5x
∵ BE=10
∴ 5x=10,x=2
∴ DF=2×2=4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一根长为22cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是 ( ).

A. 9cm≤h≤10cm B. 10cm≤h≤11cm C. 12cm≤h≤13cm D. 8cm≤h≤9cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进甲、乙两种商品,购进 4 件甲种商品比购进 5 件乙种商品少用 10 元,购 进 20 件甲种商品和 10 件乙种商品共用去 160 元.
(1)求甲、乙两种商品每件进价分别是多少元?
(2)若该商店购进甲、乙两种商品共 140 件,都标价 10 元出售,售出一部分降价促销, 以标价的八折售完所有剩余商品,以 10 元售出的商品件数比购进甲种商品件数少 20 件,该商店此次购进甲、乙两种商品降价前后共获利不少于 420 元,求至少购进甲种商品多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC、BD是它的对角线,∠ABC=∠ADC=90°,∠BCD是锐角.
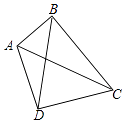
(1)写出这个四边形的一条性质并证明你的结论.
(2)若BD=BC,证明: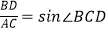 .
.
(3)①若AB=BC=4,AD+DC=6,求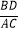 的值.
的值.
②若BD=CD,AB=6,BC=8,求sin∠BCD的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:

(1)斜边AB的长;
(2)△ABC的面积;
(3)高CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点 A(2,0),B(0,4),点 C 在第一象限.
(1)如图 1,连接 AB、BC、AC,∠OBC=90°,∠BAC=2∠ABO,求点 C 的坐标;
(2)动点 P 从点 B 出发,以每秒 2 个单位的速度沿 x 轴负方向运动,连接 AP,设 P 点的 运动时间为 t 秒,△AOP 的面积为 S,用含 t 的式子表示 S,并直接写出 t 的取值范围;
(3)如图 2,在(1)条件下,点 P 在线段 OB 上,连接 AP、PC,AB 与 PC 相交于点 Q,当S=3, ∠BAC=∠BPC 时,求△ACQ 的面积.
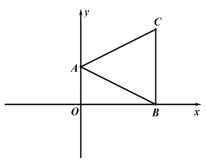
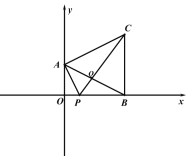
图 1 图 2
相关试题

