搜索
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=6cm，CD⊥AB于D，求：
（1）斜边AB的长；
（2）△ABC的面积；
（3）高CD的长．
参考答案：
【答案】（1）AB=10cm；（2）△ABC的面积=24cm2；（3）CD=2.4．
【解析】试题分析：
（1）利用勾股定理直接求解即可；
（2）利用三角形面积公式计算即可；
（3）由△ACB的面积为定值，可得
ACBC=CDAD，进而可求出高CD的长．
试题解析：
（1）∵在Rt△ABC中，∠ACB=90°，AC=8cm，BC=6cm，
∴AB=
=10cm；
（2）△ABC的面积=ACBC=×6×8=24cm2；
（3）由（2）可知ACBC=CDAB=24，
∴CD=
=2.4．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店购进甲、乙两种商品，购进 4 件甲种商品比购进 5 件乙种商品少用 10 元，购 进 20 件甲种商品和 10 件乙种商品共用去 160 元.
（1）求甲、乙两种商品每件进价分别是多少元？
（2）若该商店购进甲、乙两种商品共 140 件，都标价 10 元出售，售出一部分降价促销， 以标价的八折售完所有剩余商品，以 10 元售出的商品件数比购进甲种商品件数少 20 件，该商店此次购进甲、乙两种商品降价前后共获利不少于 420 元，求至少购进甲种商品多少件？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC 中，∠ACB=90° AD 是它的角平分线，EB⊥AB 于点 B 且交 AD 的延长线于点 E.
（1）如图 1，求证：BD=BE
（2）如图 2，过点 E 作 EF⊥BC 于点 F, CF:BF=5:3, BE=10,求 DF 的长.
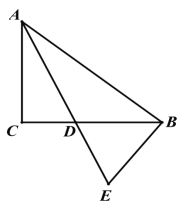
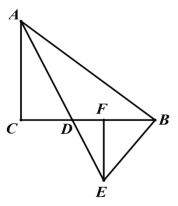
图 1 图 2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，AC、BD是它的对角线，∠ABC=∠ADC=90°，∠BCD是锐角．
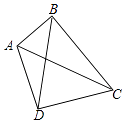
（1）写出这个四边形的一条性质并证明你的结论．
（2）若BD=BC，证明：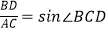
．
（3）①若AB=BC=4，AD+DC=6，求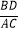
的值．
②若BD=CD，AB=6，BC=8，求sin∠BCD的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点 A(2，0)，B(0，4),点 C 在第一象限.
（1）如图 1，连接 AB、BC、AC，∠OBC=90°，∠BAC=2∠ABO,求点 C 的坐标；
（2）动点 P 从点 B 出发，以每秒 2 个单位的速度沿 x 轴负方向运动，连接 AP，设 P 点的 运动时间为 t 秒，△AOP 的面积为 S，用含 t 的式子表示 S，并直接写出 t 的取值范围；
（3）如图 2，在（1）条件下，点 P 在线段 OB 上，连接 AP、PC,AB 与 PC 相交于点 Q,当S=3, ∠BAC=∠BPC 时，求△ACQ 的面积.
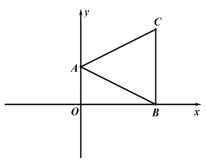
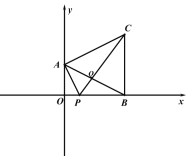
图 1 图 2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A（﹣2，0）、B（4，0）、C（3，3）在抛物线y=ax2+bx+c上，点D在y轴上，且DC⊥BC，∠BCD绕点C顺时针旋转后两边与x轴、y轴分别相交于点E、F．
（1）求抛物线的解析式；
（2）CF能否经过抛物线的顶点？若能，求出此时点E的坐标；若不能，说明理由；
（3）若△FDC是等腰三角形，求点F的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】把正整数1，2，3，4，2016排列成如图所示的形式.
（1）用一个矩形随意框住4个数，把其中最小的数记为
,另三个数用含式子表示出来，当被框住的4个数之和等于418时，值是多少？（2）被框住的4个数之和能否等于724？如果能，请求出此时x值；如果不能，请说明理由.
相关试题
