【题目】如图,四边形ABCD中,AC、BD是它的对角线,∠ABC=∠ADC=90°,∠BCD是锐角.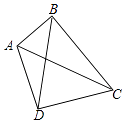
(1)写出这个四边形的一条性质并证明你的结论.
(2)若BD=BC,证明: ![]() .
.
(3)①若AB=BC=4,AD+DC=6,求 ![]() 的值.
的值.
②若BD=CD,AB=6,BC=8,求sin∠BCD的值.
参考答案:
【答案】
(1)
解:结论:AB2+BC2=AD2+DC2.
理由:∵∠ABC=∠ADC=90°,
∴AB2+BC2=AC2,BC2+DC2=AC2,
∴AB2+BC2=AD2+DC2
(2)
解:如图1中,过点B作AD的垂线BE交DA的延长线于点E,
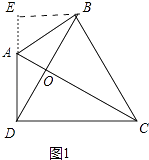
∵∠ABC=∠ADC=90°,
∴∠ADC+∠ABC=180°,
∴四边形ABCD四点共圆,
∴∠BDE=∠ACB,∠EAB=∠BCD,
∵∠BED=∠ABC=90°,
∴△BED∽△ABC,
∴ ![]() =
= ![]() =sin∠EAB=sin∠BCD
=sin∠EAB=sin∠BCD
(3)
解:①如图2中,过点B作BF⊥BD交DC的延长线于F.
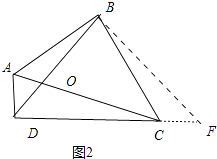
∵∠ABC=∠DBF=90°,∠BAD+∠BCD+∠ABC+∠ADC=360°,∠ABC+∠ADC=180°,
∴∠BAD=180°﹣∠BCD=∠BCF,
∵∠BCF=∠BAD,BC=BA,
∴△DAB≌△CBF,
∴BD=BF,AD=CF,
∵∠DBF=90°,
∴△BDF是等腰直角三角形,
∴BD= ![]() DF,
DF,
∵AD+CD=6,
∴CF+CD=DF=6,
∴BD=3 ![]() ,AC=
,AC= ![]() =4
=4 ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() .
.
②当BD=CD时,如图3中,过点B作MN∥DC,过点C作CN⊥MN,垂足为NM延长BA交MN于点N,则四边形DCNM是矩形,△ABM∽△BCN,
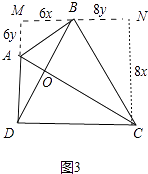
∴ ![]() ,设AM=6y,BN=8y,BM=6x,CN=8x,
,设AM=6y,BN=8y,BM=6x,CN=8x,
在Rt△BDM中,BD= ![]() =10x,
=10x,
∵BD=DC,
∴10x=6x+8y,
∴x=2y,
在Rt△DABM中,AB= ![]() =6
=6 ![]() y,
y,
∴sin∠BCD=sin∠MAB= ![]() =
= ![]() =
= ![]()
【解析】(1)结论:AB2+BC2=AD2+DC2 , 根据勾股定理即可证明.(2)如图1中,过点B作AD的垂线BE交DA的延长线于点E,只要证明△BED∽△ABC,即可解决问题.(3)①如图2中,过点B作BF⊥BD交DC的延长线于F.只要证明△DAB≌△CBF,推出DF=AD+CD=6,求出BD、AC即可.
②当BD=CD时,如图3中,过点B作MN∥DC,过点C作CN⊥MN,垂足为NM延长BA交MN于点N,则四边形DCNM是矩形,△ABM∽△BCN,所以 ![]() ,设AM=6y,BN=8y,BM=6x,CN=8x,通过BD=DC,列出方程求出x、y的关系,求出AB,即可解决问题.
,设AM=6y,BN=8y,BM=6x,CN=8x,通过BD=DC,列出方程求出x、y的关系,求出AB,即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进甲、乙两种商品,购进 4 件甲种商品比购进 5 件乙种商品少用 10 元,购 进 20 件甲种商品和 10 件乙种商品共用去 160 元.
(1)求甲、乙两种商品每件进价分别是多少元?
(2)若该商店购进甲、乙两种商品共 140 件,都标价 10 元出售,售出一部分降价促销, 以标价的八折售完所有剩余商品,以 10 元售出的商品件数比购进甲种商品件数少 20 件,该商店此次购进甲、乙两种商品降价前后共获利不少于 420 元,求至少购进甲种商品多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,∠ACB=90° AD 是它的角平分线,EB⊥AB 于点 B 且交 AD 的延长线于点 E.
(1)如图 1,求证:BD=BE
(2)如图 2,过点 E 作 EF⊥BC 于点 F, CF:BF=5:3, BE=10,求 DF 的长.
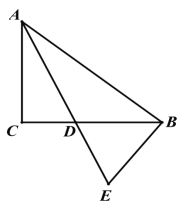
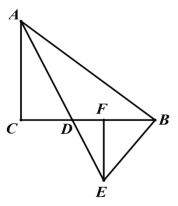
图 1 图 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,CD⊥AB于D,求:

(1)斜边AB的长;
(2)△ABC的面积;
(3)高CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点 A(2,0),B(0,4),点 C 在第一象限.
(1)如图 1,连接 AB、BC、AC,∠OBC=90°,∠BAC=2∠ABO,求点 C 的坐标;
(2)动点 P 从点 B 出发,以每秒 2 个单位的速度沿 x 轴负方向运动,连接 AP,设 P 点的 运动时间为 t 秒,△AOP 的面积为 S,用含 t 的式子表示 S,并直接写出 t 的取值范围;
(3)如图 2,在(1)条件下,点 P 在线段 OB 上,连接 AP、PC,AB 与 PC 相交于点 Q,当S=3, ∠BAC=∠BPC 时,求△ACQ 的面积.
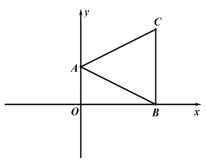
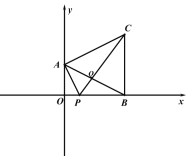
图 1 图 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(﹣2,0)、B(4,0)、C(3,3)在抛物线y=ax2+bx+c上,点D在y轴上,且DC⊥BC,∠BCD绕点C顺时针旋转后两边与x轴、y轴分别相交于点E、F.

(1)求抛物线的解析式;
(2)CF能否经过抛物线的顶点?若能,求出此时点E的坐标;若不能,说明理由;
(3)若△FDC是等腰三角形,求点F的坐标.
相关试题

