【题目】△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,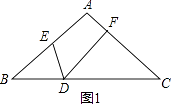
求证:DECD=DFBE
(2)D为BC中点如图2,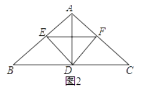
连接EF.
①求证:ED平分∠BEF;
②若四边形AEDF为菱形,求∠BAC的度数及 ![]() 的值.
的值.
参考答案:
【答案】
(1)
证明:∵△ABC中,AB=AC,
∴∠B=∠C.
∵∠B+∠BDE+∠DEB=180°,∠BDE+∠EDF+∠FDC=180°,∠EDF=∠B,
∴∠FDC=∠DEB,
∴△BDE∽△CFD,
∴ ![]() ,
,
即DECD=DFBE
(2)
解:①由(1)证得△BDE∽△CFD,
∴ ![]() ,
,
∵D为BC中点,
∴BD=CD,
∴ ![]() =
= ![]() ,
,
∵∠B=∠EDF,
∴△BDE∽△DEF,
∴∠BED=∠DEF,
∴ED平分∠BEF;②∵四边形AEDF为菱形,
∴∠AEF=∠DEF,
∵∠BED=∠DEF,
∴∠AEF=60°,
∵AE=AF,
∴∠BAC=60°,
∵∠BAC=60°,
∴△ABC是等边三角形,
∴∠B=60°,
∴△BED是等边三角形,
∴BE=DE,
∵AE=DE,
∴AE= ![]() AB,
AB,
∴ ![]() =
= ![]()
【解析】(1)先根据题意得出△BDE∽△CFD,再由相似三角形的性质即可得出结论;(2)①根据相似三角形的性质得到 ![]() ,推出△BDE∽△DEF,根据相似三角形的性质即可得到结论;②由四边形AEDF为菱形,得到∠AEF=∠DEF,于是得到∠AEF=60°,推出△ABC是等边三角形,△BED是等边三角形,得到BE=DE,即可得到结论.
,推出△BDE∽△DEF,根据相似三角形的性质即可得到结论;②由四边形AEDF为菱形,得到∠AEF=∠DEF,于是得到∠AEF=60°,推出△ABC是等边三角形,△BED是等边三角形,得到BE=DE,即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2015本溪,第9题,3分)如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线
 (
(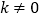 )上,则k的值为( )
)上,则k的值为( )
A. 4 B. ﹣2 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(A2013防城港)如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下: 甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
A.甲正确,乙错误
B.乙正确,甲错误
C.甲、乙均正确
D.甲、乙均错误 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空:
(1)A地与B地之间的距离是多少千米;
(2)甲车由A地前往B地时所对应的s与t的函数解析式及定义域;
(3)甲车由A地前往B地比乙车由A地前往B地多用了多少小时.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的5×5的方格纸中,每个小正方形的边长为1,点A、B、C均为格点(格点是指每个小正方形的顶点).
(1)按下列要求画图:
①标出格点D,使CD∥AB,并画出线段CD;
②标出格点E,使CE⊥AB,并画出线段CE.
(2)CD与CE的关系是 .
(3)计算△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是⊙O内接正三角形,将△ABC绕点O顺时针旋转30°得到△DEF,DE分别交AB,AC于点M,N,DF交AC于点Q,则有以下结论:①∠DQN=30°;②△DNQ≌△ANM;③△DNQ的周长等于AC的长;④NQ=QC.其中正确的结论是 ①②③ .(把所有正确的结论的序号都填上)
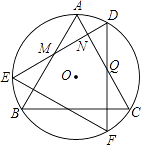
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,﹣3),顶点为D.

(1)求出抛物线y=x2+bx+c的表达式;
(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①当m为何值时,四边形PEDF为平行四边形.
②设四边形OBFC的面积为S,求S的最大值.
相关试题

