【题目】在如图所示的5×5的方格纸中,每个小正方形的边长为1,点A、B、C均为格点(格点是指每个小正方形的顶点).
(1)按下列要求画图:
①标出格点D,使CD∥AB,并画出线段CD;
②标出格点E,使CE⊥AB,并画出线段CE.
(2)CD与CE的关系是 .
(3)计算△ABC的面积.

参考答案:
【答案】(1)①画图见解析;②画图见解析;(2) CD⊥CE,CD=CE;(3)4.
【解析】
(1)直接利用网格得出AB的平行线CD;直接利用网格结合垂线的作法得出答案;
(2)可通过勾股定理证明CD⊥CE.
(3)根据三角形的面积为大正方形减去三个小直角三角形即可.
(1)①如图;
②如图;
(2) CD⊥CE,CD=CE
(3) S△ABC=3×3![]() ×3×1
×3×1![]() ×2×2
×2×2![]() ×3×1=4.
×3×1=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(A2013防城港)如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下: 甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
A.甲正确,乙错误
B.乙正确,甲错误
C.甲、乙均正确
D.甲、乙均错误 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空:
(1)A地与B地之间的距离是多少千米;
(2)甲车由A地前往B地时所对应的s与t的函数解析式及定义域;
(3)甲车由A地前往B地比乙车由A地前往B地多用了多少小时.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,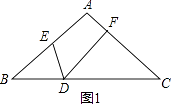
求证:DECD=DFBE
(2)D为BC中点如图2,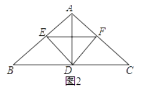
连接EF.
①求证:ED平分∠BEF;
②若四边形AEDF为菱形,求∠BAC的度数及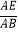 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是⊙O内接正三角形,将△ABC绕点O顺时针旋转30°得到△DEF,DE分别交AB,AC于点M,N,DF交AC于点Q,则有以下结论:①∠DQN=30°;②△DNQ≌△ANM;③△DNQ的周长等于AC的长;④NQ=QC.其中正确的结论是 ①②③ .(把所有正确的结论的序号都填上)
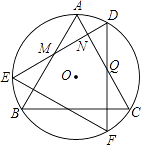
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,﹣3),顶点为D.

(1)求出抛物线y=x2+bx+c的表达式;
(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①当m为何值时,四边形PEDF为平行四边形.
②设四边形OBFC的面积为S,求S的最大值. -
科目: 来源: 题型:
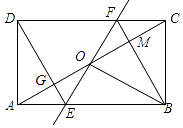
查看答案和解析>>【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S四边形DGOF=2:7.其中正确结论的个数是( )
A.4个
B.3个
C.2个
D.1个
相关试题

