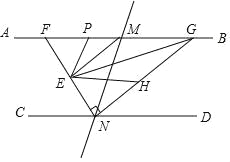
【题目】如图,直线AB∥CD,直线MN与AB,CD分别交于点M,N,ME,NE分别是∠AMN与∠CNM的平分线,NE交AB于点F,过点N作NG⊥EN交AB于点G.
(1)求证:EM∥NG;
(2)连接EG,在GN上取一点H,使∠HEG=∠HGE,作∠FEH的平分线EP交AB于点P,求∠PEG的度数.
参考答案:
【答案】(1)证明见解析;(2)45°.
【解析】
(1)根据平行线的性质以及角平分线得到定义,即可得出∠MEN=90°,再根据NG⊥EN,即可得到∠MEN+∠ENH=180°,进而得到EM∥NG;
(2)先设∠HEG=x,则∠HGE=∠MEG=x,∠NEH=90°-2x,根据EP平分∠FEH,可得∠FEH=2(∠PEG+x),再根据∠FEH+∠HEN=180°,可得方程2(∠PEG+x)+90°-2x=180°,进而解得∠PEG.
解:(1)∵AB∥CD,
∴∠AMN+∠CNM=180°,
∵ME,NE分别是∠AMN与∠CNM的平分线,
∴∠EMN=![]() ∠AMN,∠ENM=
∠AMN,∠ENM=![]() ∠MNC,
∠MNC,
∴∠EMN+∠ENM=90°,即∠MEN=90°,
又∵NG⊥EN,
∴∠MEN+∠ENH=180°,
∴EM∥NG;
(2)设∠HEG=x,则∠HGE=∠MEG=x,∠NEH=90°﹣2x,
∵EP平分∠FEH,
∴∠FEH=2∠PEH=2(∠PEG+x),
又∵∠FEH+∠HEN=180°,
∴2(∠PEG+x)+90°﹣2x=180°,
解得∠PEG=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知直线y=﹣
 x+4与y轴交于A点,与x轴交于B点,C点的坐标为(﹣2,0).
x+4与y轴交于A点,与x轴交于B点,C点的坐标为(﹣2,0).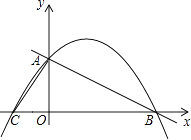
(1)求证:直线AB⊥AC;
(2)求经过A,B,C三点的抛物线l的解析式和对称轴;
(3)在直线AB上方的抛物线l上,是否存在一点P,使直线AB平分∠PBC?
若存在,请求出P点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为
-
科目: 来源: 题型:
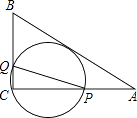
查看答案和解析>>【题目】如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是( )
A.4.75
B.4.8
C.5
D.4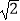
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
A.
B.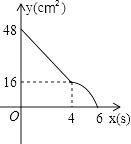
C.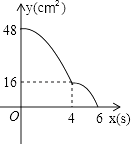
D.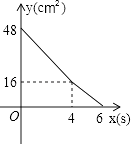
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列分式方程:
(1)
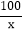 =
=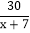 ; (2)
; (2)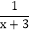 -
-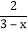 =
=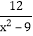
-
科目: 来源: 题型:
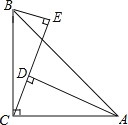
查看答案和解析>>【题目】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)求证:△ACD≌△CBE;
(2)若AD=12,DE=7,求BE的长.
相关试题

