【题目】在学校开展的数学活动课上,小明和小刚制作了一个正三楼锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下每人投掷三棱锥两次,并记录底面的数字,如果两次所掷数字的和为单数,那么算小明赢,如果两欢所掷数字的和为偶数,那么算小明赢;
(1)请用列表或者面树状围的方法表示上述游戏中的所有可能结果.
(2)请分别隶出小明和小刚能赢的概率,并判新游戏的公平性.

参考答案:
【答案】(1)见解析;(2)小明获胜的概率为![]() 、小刚获胜的概率为
、小刚获胜的概率为![]() ,此游戏对两人是公平的.
,此游戏对两人是公平的.
【解析】
见解析.
(1)列表如下:
1 | 2 | 3 | 4 | |
1 | 2 | 3 | 4 | 5 |
2 | 3 | 4 | 5 | 6 |
3 | 4 | 5 | 6 | 7 |
4 | 5 | 6 | 7 | 8 |
(2)从图表可知,共有16种等可能的情况,其中两次所掷数字的和为单数的情况有8种,和为偶数的有8种,
所以小明获胜的概率为![]() 、小刚获胜的概率为
、小刚获胜的概率为![]() ,
,
故此游戏对两人是公平的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知动点A在函数y=
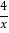 (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.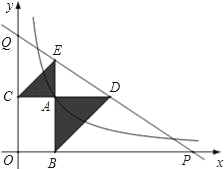
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BE=CF.

(2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF=4.求GH的长.

(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4. 直接写出下列两题的答案:
①如图3,矩形ABCD由2个全等的正方形组成,求GH的长;

②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).
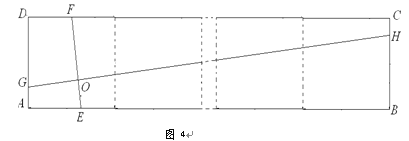
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O为△ABC的外接圆,AB=AC,直线MN与⊙O相切于点C,弦BD∥MN,AC与BD相交于点E.

(1)求证:△ABE ≌ △ACD;
(2)若AB = 5,BC = 3,求AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2013年初春,我国西北部分省区发生了雪灾,造成通讯受阻.如图,现有某处山坡上一座发射塔被冰雪从C处压折,塔尖恰好落在坡面上的点B处,在B处测得点C的仰角为45°,塔基A的俯角为30°,又测得斜坡上点A到点B的坡面距离AB为20米,求折断前发射塔的高.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为等边△ABC外一点,AH垂直平分PC于点H,∠BAP的平分线交PC于点D.

(1)求证:DP=DB;
(2)求证:DA+DB=DC;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰
 中,
中, ,点A、B分别在坐标轴上.
,点A、B分别在坐标轴上.
(1)如图①,若
 ,
, ,求C点的坐标;
,求C点的坐标;(2)如图②,若点A的坐标为
 ,点B在y轴的正半轴上运动时,分别以OB,AB为边在第一,第二象限作等腰
,点B在y轴的正半轴上运动时,分别以OB,AB为边在第一,第二象限作等腰 ,等腰
,等腰 ,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度是否变化?如果不变求出PB值,如果变化求PB的取值范围.
,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度是否变化?如果不变求出PB值,如果变化求PB的取值范围.
相关试题

