【题目】三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(-3,1),B(-2,4).

(1)请你在方格中建立直角坐标系,并写出C点的坐标;
(2)把△ABC向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 .
(3)在x轴上存在一点D,使△DB1C1的面积等于3,求满足条件的点D的坐标.
参考答案:
【答案】(1)画图见解析,C(1,1);(2)画图见解析,(a+2,b-1);(3)D(1,0)或(5,0)
【解析】
(1)根据点A、B的坐标和直角坐标系的特点建立直角坐标系;
(2)分别将点A、B、C向下平移1个单位长度,再向右平移2个单位长度,然后顺次连接各点,并写出点P的对应点P1的坐标;
(3)根据三角形的面积求出C1D的长度,再分两种情况求出OD的长度,然后写出点D的坐标即可.
解:(1)直角坐标系如图所示,
C点坐标(1,1);

(2)△A1B1C1如图所示,
点P1坐标(a+2,b-1);
故答案为:(a+2,b-1);
(3)设点D的坐标为(a,0),则:
△DB1C1的面积=![]() C1D×OB1=3,
C1D×OB1=3,
即![]() |a-3|×3=3,
|a-3|×3=3,
解得:a=1或a=5,
综上所述,点D的坐标为(1,0)或(5,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下面的解答过程补充完整:如图,点
 在
在 上,点
上,点 在
在 上,
上, ,
, .试说明:
.试说明: ∥
∥ .
.
解:∵
 (已知)
(已知) ( )
( )∴
 (等量代换)
(等量代换)∴ ______∥_______( )
∴
 ( )
( )∵
 (已知)
(已知)∴
 ( )
( )∴
 ∥
∥ ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,且AN=8,BN=6,AC=16,则MN的长是()

A. 4B. 3C. 2.5D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
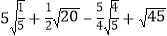 ;
; (2)
 ;
; (3)
 ;
;(4)先化简,再求值:(
 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2+bx+
 经过A(1,0),B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边三角形ABC.
经过A(1,0),B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边三角形ABC.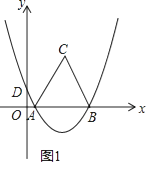
(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM=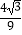 S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长.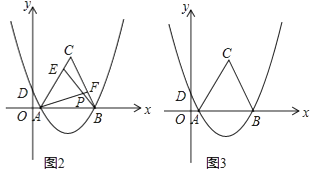
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程ax2﹣3x+3=0有两个不等实根,则a的取值范围是( )
A.a< 且a≠0
且a≠0
B.a>﹣ 且a≠0
且a≠0
C.a>﹣
D.a<
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将矩形纸片ABCD沿对角线BD向上折叠,点C落在点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
图1

图2

相关试题

