【题目】关于x的一元二次方程x2﹣2kx+k2+k﹣2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若k为正整数,求k的值及此时方程的根.
参考答案:
【答案】(1)k<2;(2)k=1,x=0或x=2.
【解析】
(1)由方程有两个不相等的实数根得出其判别式的值大于0,据此列出关于k的不等式,解之可得;
(2)再所求k的范围内取值代入方程,再进一步解方程可得答案.
解:(1)根据题意知△=(﹣2k)2﹣4×1×(k2+k﹣2)>0,
即﹣4k+8>0,
解得k<2;
(2)∵k<2且k为正整数,
∴k=1,
∴x2﹣2x=0,
解得x=0或x=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋中装有红色、白色玻璃球共60个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在25%左右,则口袋中红色球可能有()
A.5个
B.10个
C.15个
D.45个 -
科目: 来源: 题型:
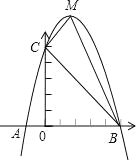
查看答案和解析>>【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积
 .
.(3)在坐标轴上,是否存在点N,满足△BCN为直角三角形?如存在,请直接写出所有满足条件的点N.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)12﹣(﹣18)+(﹣7)﹣15;
(2)(﹣8)+4÷(﹣2);
(3)(﹣10)÷(﹣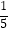 )×5;
)×5;
(4)[1﹣(1﹣0.5× )]×[2﹣(﹣3)2].
)]×[2﹣(﹣3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,四边形ABCD(图1)与四边形EFGH(图2)的形状、大小完全相同.
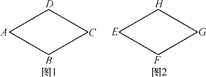
(1)请从下列序号中选择正确选项的序号填写;
①点E,F,G,H;②点G,F,E,H;③点E,H,G,F;④点G,H,E,F.
如果图1经过一次平移后得到图2,那么点A,B,C,D的对应点分别是 ;
如果图1经过一次轴对称后得到图2,那么点A,B,C,D的对应点分别是 ;
如果图1经过一次旋转后得到图2,那么点A,B,C,D的对应点分别是 ;
(2)如果图1经过绕某点旋转180°后得到图2,请画出旋转中心(保留画图痕迹,不写画法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)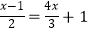
(2)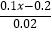 ﹣
﹣  =3.
=3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB和CD的公共部分BD=
 AB=
AB=  CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长. 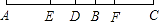
相关试题

