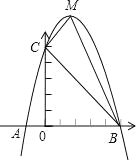
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积![]() .
.
(3)在坐标轴上,是否存在点N,满足△BCN为直角三角形?如存在,请直接写出所有满足条件的点N.
参考答案:
【答案】(1)y=﹣x2+4x+5(2)15(3)存在,(0,0)或(0,﹣5)或(﹣5,0)
【解析】
试题分析:(1)把A(﹣1,0),C(0,5),(1,8)三点代入二次函数解析式,解方程组即可.
(2)先求出M、B、C的坐标,根据![]() 即可解决问题.
即可解决问题.
(3)分三种情①C为直角顶点;②B为直角顶点;③N为直角顶点;分别求解即可.
试题解析:(1)∵二次函数y=ax2+bx+c的图象经过A(﹣1,0),C(0,5),(1,8),
则有: ,
,
解得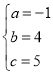 .
.
∴抛物线的解析式为y=﹣x2+4x+5.
(2)令y=0,得(x﹣5)(x+1)=0,x1=5,x2=﹣1,
∴B(5,0).
由y=﹣x2+4x+5=﹣(x﹣2)2+9,得顶点M(2,9)
如图1中,作ME⊥y轴于点E,
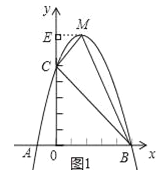
可得![]() =
=![]() (2+5)×9﹣
(2+5)×9﹣![]() ×4×2﹣
×4×2﹣![]() ×5×5=15.
×5×5=15.
(3)存在.如图2中,
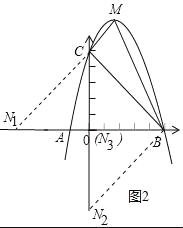
∵OC=OB=5,
∴△BOC是等腰直角三角形,
①当C为直角顶点时,N1(﹣5,0).
②当B为直角顶点时,N2(0,﹣5).
③当N为直角顶点时,N3(0,0).
综上所述,满足条件的点N坐标为(0,0)或(0,﹣5)或(﹣5,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率 -
科目: 来源: 题型:
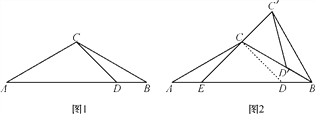
查看答案和解析>>【题目】如图1,△ABC中,AC=BC,∠A=30°,点D在AB边上,且∠ADC=45°.
(1)求∠BCD的度数;
(2)将图1中的△BCD绕点B顺时针旋转得到△BC′D′,当点D′恰好落在BC边上时,如图2所示,连接C′C并延长交AB于点E.
①求∠C′CB的度数;
②求证:△C′BD′≌△CAE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋中装有红色、白色玻璃球共60个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在25%左右,则口袋中红色球可能有()
A.5个
B.10个
C.15个
D.45个 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)12﹣(﹣18)+(﹣7)﹣15;
(2)(﹣8)+4÷(﹣2);
(3)(﹣10)÷(﹣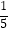 )×5;
)×5;
(4)[1﹣(1﹣0.5× )]×[2﹣(﹣3)2].
)]×[2﹣(﹣3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2﹣2kx+k2+k﹣2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若k为正整数,求k的值及此时方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,四边形ABCD(图1)与四边形EFGH(图2)的形状、大小完全相同.
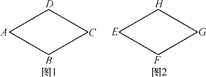
(1)请从下列序号中选择正确选项的序号填写;
①点E,F,G,H;②点G,F,E,H;③点E,H,G,F;④点G,H,E,F.
如果图1经过一次平移后得到图2,那么点A,B,C,D的对应点分别是 ;
如果图1经过一次轴对称后得到图2,那么点A,B,C,D的对应点分别是 ;
如果图1经过一次旋转后得到图2,那么点A,B,C,D的对应点分别是 ;
(2)如果图1经过绕某点旋转180°后得到图2,请画出旋转中心(保留画图痕迹,不写画法).
相关试题

