搜索
【题目】如图，等边三角形OAB的一边OA在x轴上，双曲线y= 
在第一象限内的图象经过OB边的中点C，则点B的坐标是 ． 
参考答案：
【答案】（2，2 
）
【解析】解：过点C作CD⊥OA于点D，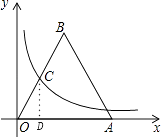 
∵△OAB是等边三角形，
∴∠AOB=60°，
∴∠OCD=30°，
设OD=x，则OC=2OD=2x，
∴CD= 
= x，
∴点C的坐标为：（x， x），
∵双曲线y= 
在第一象限内的图象经过OB边上的点C，
∴ x= ，
解得：x=±1（负值舍去），
∴点C（1， ）．
则B的坐标是（2，2 ）
故答案是：（2，2 ）．
【考点精析】本题主要考查了等边三角形的性质的相关知识点，需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c（a＞0）经过点M（﹣1，2）和点N（1，﹣2），交x轴于A，B两点，交y轴于C，则：
①a+c=0；
②无论a取何值，此二次函数图象与x轴必有两个交点，函数图象截x轴所得的线段长度必大于2；
③当函数在x＜
时，y随x的增大而减小；
④当﹣1＜m＜n＜0时，m+n＜
；
⑤若a=1，则OAOB=OC2 ．
以上说法正确的有（ ）
A.①②③④⑤
B.①②④⑤
C.②③④
D.①②③⑤ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点C是线段AB的中点，CD平分
，CE平分
，CD=CE.（1）求证：
（2）若
，求
的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ABC=90°，AB=BC=
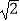，将△ABC绕点C逆时针旋转60°，得到△MNC，连接BM，则BM的长是 .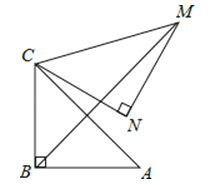
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AB=AD=6，AB⊥BC，AD⊥CD，∠BAD=60°，点M、N分别在AB、AD边上，若AM：MB=AN：ND=1：2．则 cos∠MCN= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知Rt△ABC≌Rt△ADE，其中∠ACB=∠AED=90°．
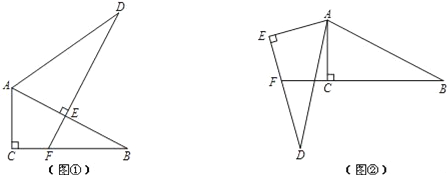
（1）将这两个三角形按图①方式摆放，使点E落在AB上，DE的延长线交BC于点F．求证：BF+EF=DE；
（2）改变△ADE的位置，使DE交BC的延长线于点F（如图②），则（1）中的结论还成立吗？若成立，加以证明；若不成立，写出此时BF、EF与DE之间的等量关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】学习了三角形全等的判定方法和直角三角形全等的判定方法后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情况进行研究.
（初步思考）我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，
，然后，对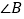
进行分类，可分为“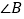是直角，钝角，锐角”三种情况进行探索.（深入探究）（1）当
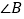是直角时，如图①，在△ABC和△DEF中，AC=DF，BC=EF，
，根据 可以知道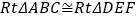
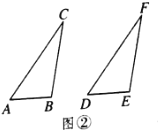
.（2）当
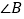是钝角时，如图②，在△ABC和△DEF中，AC=DF，BC=EF，，且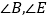
都是钝角，求证：
.（3）当
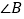是锐角时，在△ABC和△DEF中，AC=DF，BC=EF，，且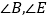都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等（不写做法，保留作图痕迹）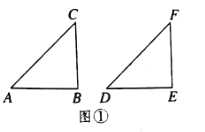
相关试题
