【题目】已知二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),交x轴于A,B两点,交y轴于C,则:
①a+c=0;
②无论a取何值,此二次函数图象与x轴必有两个交点,函数图象截x轴所得的线段长度必大于2;
③当函数在x< ![]() 时,y随x的增大而减小;
时,y随x的增大而减小;
④当﹣1<m<n<0时,m+n< ![]() ;
;
⑤若a=1,则OAOB=OC2 .
以上说法正确的有( )
A.①②③④⑤
B.①②④⑤
C.②③④
D.①②③⑤
参考答案:
【答案】B
【解析】解:∵二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),
∴ ![]() ,
,
∴①+②得:a+c=0;故①正确;
∵a=﹣c
∴b2﹣4ac>0,
∴无论a取何值,此二次函数图象与x轴必有两个交点,
∵|x1﹣x2|= ![]() =
= ![]() ,
, ![]() =﹣1,
=﹣1,
∴ ![]() >2,
>2,
故②正确;
二次函数y=ax2+bx+c(a>0)的对称轴x=﹣ ![]() =
= ![]() ,当a>0时不能判定x<
,当a>0时不能判定x< ![]() 时,y随x的增大而减小;故③错误;
时,y随x的增大而减小;故③错误;
∵﹣1<m<n<0,a>0,
∴m+n<0, ![]() >0,
>0,
∴m+n< ![]() ;故正确;
;故正确;
∵a=1,
∴二次函数为y=x2+bx+c,
∴OC2=c2=|x1x2|=OAOB,故正确;
故应选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索性问题:
已知:b是最小的正整数,且a、b满足(c﹣5)2+|a+b|=0,请回答问题:
(1)请直接写出a、b、c的值.a= ,b= ,c= ;
(2)数轴上a、b、c三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC.
①t秒钟过后,AC的长度为 (用t的关系式表示);
②请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿BD对折,点A落在E处,BE与CD相交于F,若AD=3,BD=6.
(1)求证:△EDF≌△CBF;
(2)求∠EBC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图只需在⊙O上任取点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( ) ①两等分 ②三等分 ③四等分 ④五等分.

A.②
B.①②
C.①②③
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB的中点,CD平分
 ,CE平分
,CE平分 ,CD=CE.
,CD=CE.(1)求证:

(2)若
 ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=
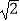 ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .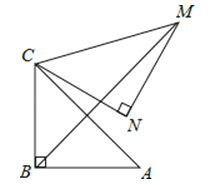
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形OAB的一边OA在x轴上,双曲线y=
 在第一象限内的图象经过OB边的中点C,则点B的坐标是 .
在第一象限内的图象经过OB边的中点C,则点B的坐标是 . 
相关试题

