【题目】在如图的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4. 
(1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),试在图中画出平面直角坐标系,并标出A、C两点的坐标;
(3)根据(2)的坐标系,以B为位似中心,做△BA2C2 , 使△BA2C2与△ABC位似,且△BA2C2与△ABC位似比为2:1,并直接写出A2的坐标. 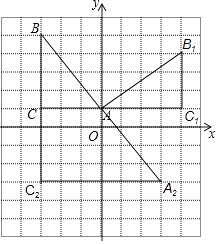
参考答案:
【答案】
(1)解:如图所示:△AB1C1,即为所求
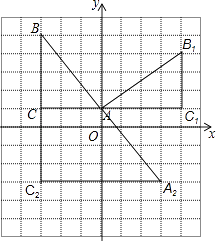
(2)解:如图所示:A(0、1)、C(﹣3、1)

(3)解:如图所示:△BA2C2,即为所求,A2(3、﹣3 )
【解析】(1)直接利用旋转的性质得出对应点位置进而得出答案;(2)利用B点坐标得出原点位置,进而得出A、C两点的坐标;(3)利用位似图形的性质得出对应点位置,进而得出答案.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对作图-位似变换的理解,了解对应点到位似中心的距离比就是位似比,对应线段的比等于位似比,位似比也有顺序;已知图形的位似图形有两个,在位似中心的两侧各有一个.位似中心,位似比是它的两要素.
-
科目: 来源: 题型:
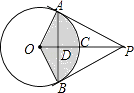
查看答案和解析>>【题目】如图,P是⊙O外一点,PA和PB分别切⊙O于A、B两点,已知⊙O的半径为6cm,∠PAB=60°,若用图中阴影部分以扇形围成一个圆锥的侧面,则这个圆锥的高为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】父亲节快到了,明明准备为爸爸煮四个大汤圆作早点:一个芝麻馅,一个水果馅,两个花生馅,四个汤圆除内部馅料不同外,其它一切均相同.
(1)求爸爸吃前两个汤圆刚好都是花生馅的概率;
(2)若给爸爸再增加一个花生馅的汤圆,则爸爸吃前两个汤圆都是花生馅的可能性是否会增大?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF.
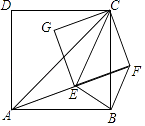
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,反比例函数y=
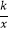 (x>0)的图象经过点A(2
(x>0)的图象经过点A(2 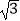 ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D. 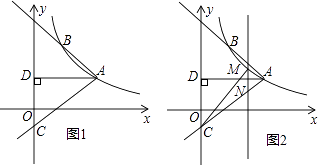
(1)求k的值;
(2)求tan∠DAC的值及直线AC的解析式;
(3)如图2,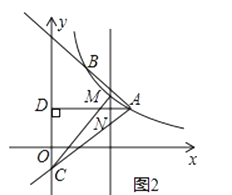
M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
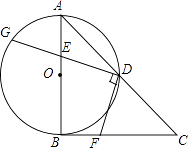
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
相关试题

