【题目】如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F. 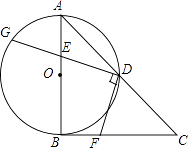
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
参考答案:
【答案】
(1)证明:连接BD,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠A=∠C=45°,
∵AB为圆O的直径,
∴∠ADB=90°,即BD⊥AC,
∴AD=DC=BD= ![]() AC,∠CBD=∠C=45°,
AC,∠CBD=∠C=45°,
∴∠A=∠FBD,
∵DF⊥DG,
∴∠FDG=90°,
∴∠FDB+∠BDG=90°,
∵∠EDA+∠BDG=90°,
∴∠EDA=∠FDB,
在△AED和△BFD中,
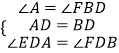 ,
,
∴△AED≌△BFD(ASA),
∴AE=BF
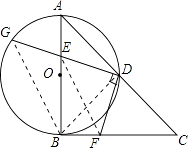
(2)证明:连接EF,BG,
∵△AED≌△BFD,
∴DE=DF,
∵∠EDF=90°,
∴△EDF是等腰直角三角形,
∴∠DEF=45°,
∵∠G=∠A=45°,
∴∠G=∠DEF,
∴GB∥EF;
(3)∵AE=BF,AE=1,
∴BF=1,
在Rt△EBF中,∠EBF=90°,
∴根据勾股定理得:EF2=EB2+BF2,
∵EB=2,BF=1,
∴EF= ![]() =
= ![]() ,
,
∵△DEF为等腰直角三角形,∠EDF=90°,
∴cos∠DEF= ![]() ,
,
∵EF= ![]() ,
,
∴DE= ![]() ×
× ![]() =
= ![]() ,
,
∵∠G=∠A,∠GEB=∠AED,
∴△GEB∽△AED,
∴ ![]() ,即GEED=AEEB,
,即GEED=AEEB,
∴ ![]() GE=2,即GE=
GE=2,即GE= ![]() ,
,
则GD=GE+ED= ![]()
【解析】(1)连接BD,由三角形ABC为等腰直角三角形,求出∠A与∠C的度数,根据AB为圆的直径,利用圆周角定理得到∠ADB为直角,即BD垂直于AC,利用直角三角形斜边上的中线等于斜边的一半,得到AD=DC=BD= ![]() AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;(2)连接EF,BG,由三角形AED与三角形BFD全等,得到ED=FD,进而得到三角形DEF为等腰直角三角形,利用圆周角定理及等腰直角三角形性质得到一对同位角相等,利用同位角相等两直线平行即可得证;(3)由全等三角形对应边相等得到AE=BF=1,在直角三角形BEF中,利用勾股定理求出EF的长,利用锐角三角形函数定义求出DE的长,利用两对角相等的三角形相似得到三角形AED与三角形GEB相似,由相似得比例,求出GE的长,由GE+ED求出GD的长即可.
AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;(2)连接EF,BG,由三角形AED与三角形BFD全等,得到ED=FD,进而得到三角形DEF为等腰直角三角形,利用圆周角定理及等腰直角三角形性质得到一对同位角相等,利用同位角相等两直线平行即可得证;(3)由全等三角形对应边相等得到AE=BF=1,在直角三角形BEF中,利用勾股定理求出EF的长,利用锐角三角形函数定义求出DE的长,利用两对角相等的三角形相似得到三角形AED与三角形GEB相似,由相似得比例,求出GE的长,由GE+ED求出GD的长即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.

(1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),试在图中画出平面直角坐标系,并标出A、C两点的坐标;
(3)根据(2)的坐标系,以B为位似中心,做△BA2C2 , 使△BA2C2与△ABC位似,且△BA2C2与△ABC位似比为2:1,并直接写出A2的坐标.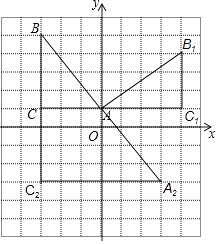
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF.
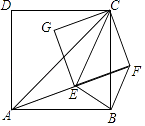
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,反比例函数y=
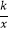 (x>0)的图象经过点A(2
(x>0)的图象经过点A(2 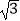 ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D. 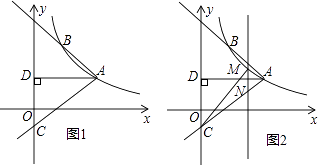
(1)求k的值;
(2)求tan∠DAC的值及直线AC的解析式;
(3)如图2,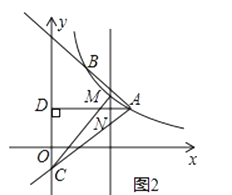
M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多能出租一次,且每辆车的日租金x(元)是5的倍数,发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆,已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)设每日净收入为w元,请写出w与x之间的函数关系式;
(3)若某日的净收入为4420元,且使游客得到实惠,则当天的观光车的日租金是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】问题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
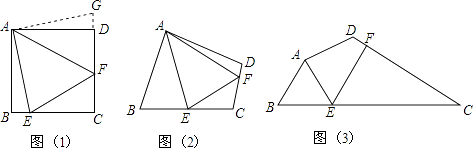
(1)【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图1证明上述结论.
(2)【类比引申】
如图2,四边形ABCD中∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD
(3)【探究应用】如图3,在某公园的同一水平面上,四条通道围成的ABCD,已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(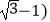 ,米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
,米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: 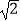 =1.41,
=1.41, 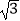 =1.73).
=1.73). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC,CD.
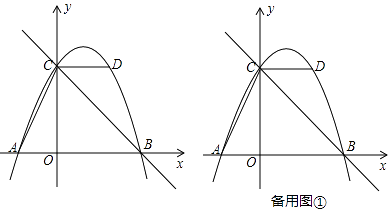
(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;
(3)点M在y轴上且位于点C上方,点N在直线BC上,点P为第一象限内抛物线上一点,若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.
相关试题

