【题目】图1是一个长为2x,宽为2y的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.

(1)图2中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法求图2中阴影部分的面积.
方法1: ;方法2: .
(3)观察图2写出![]() ,
, ![]() ,
, ![]() 三个代数式之间的等量关系: .
三个代数式之间的等量关系: .
(4)根据(3)题中的等量关系,解决如下问题: 若![]() ,
, ![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() (4)84.
(4)84.
【解析】试题分析: ![]() 图①分成了4个长为
图①分成了4个长为![]() ,宽为
,宽为![]() 的长方形,图②中的阴影部分的小正方形的边长等于
的长方形,图②中的阴影部分的小正方形的边长等于![]() ,大正方形的边长等于
,大正方形的边长等于![]()
![]() 直接利用正方形的面积公式得到②中阴影部分的面积为
直接利用正方形的面积公式得到②中阴影部分的面积为![]() 也可以用大正方形的面积减去4个长方形的面积即②
也可以用大正方形的面积减去4个长方形的面积即②![]()
![]() 利用面积之间的关系易得
利用面积之间的关系易得![]()
![]() 利用第
利用第![]() 问得出的式子进行计算即可.
问得出的式子进行计算即可.
试题解析:
(1)图②中的阴影部分的小正方形的边长为:xy;
故答案为:(xy);
(2)方法①![]() 方法②
方法②![]()
故答案为: ![]()
![]()
(3) ![]()
故答案为: ![]()
(4) ![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了节约用水,某市决定调整居民用水收费方法,规定:
①如果每户每月水不超过
 吨,每吨水收费
吨,每吨水收费 元.
元.②如果每户每月用水超过
 吨,则超过部分每吨水收费
吨,则超过部分每吨水收费 元.
元.小红看到这种收费方法后,想算算她家每月的水费,但是她不清楚家里每月的用水是否超过
 吨.
吨.(
 )如果小红家每月用水
)如果小红家每月用水 吨,水费是多少?如果每月用水
吨,水费是多少?如果每月用水 吨,水费是多少?
吨,水费是多少?(
 )如果字母
)如果字母 表示小红家每月用水的吨数,那么小红家每月的水费该如何用
表示小红家每月用水的吨数,那么小红家每月的水费该如何用 的代数式表示呢?
的代数式表示呢? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知两点A(-4,0)、B(1,0),且以AB为直径的圆交
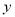 轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.
轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.
(1)求过A, B,C三点的抛物线解析式;
(2)求点D的坐标;
(3)设平行于x轴的直线交抛物线于E,F两点,问是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣2(x+1)2+1的顶点坐标是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
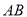 与
与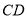 相交于点
相交于点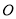 ,
, 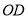 平分
平分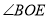 ,
, 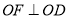 .
.(1)直接写出图中和
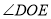 互补的角;(
互补的角;(2)
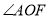 与
与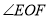 相等吗?说明理由;
相等吗?说明理由;(3)若
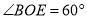 ,求
,求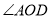 和
和 的度数.
的度数.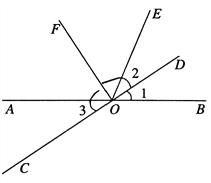
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点,连接BE、BD、DE.

(1)求证:△BED是等腰三角形;
(2)当∠BAD=°时,△BED是等腰直角三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】角平分线上的点到角两边的距离相等.这一性质在解决图形面积问题时有何妙用呢?阅读材料:已知,如图(1),在面积为S的△ABC中,BC=a,AC=b,AB=c,三条角平分线的交点O到三边的距离为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△OAC+S△OAB= BCr+
BCr+  ACr+
ACr+  ABr=
ABr=  (a+b+c)r,∴r=
(a+b+c)r,∴r= 

(1)类比推理:若面积为S的四边形ABCD的四条角平分线交于O点,如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求点O到四边的距离r;
(2)理解应用:如图(3),在四边形ABCD中,AB∥DC,AB=21,CD=11,AD=BC=13,对角线BD=20,点O1与O2分别为△ABD与△BCD的三条角平分线的交点,设它们到各自三角形三边的距离为r1和r2 , 求 的值.
的值.
相关试题

