【题目】如图是抛物线![]() 图象的一部分,抛物线的顶点坐标
图象的一部分,抛物线的顶点坐标![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,下列结论:
两点,下列结论:
①![]() ;
;
②![]() ;
;
③方程![]() 有两个相等的实数根;
有两个相等的实数根;
④抛物线与![]() 轴的另一个交点是
轴的另一个交点是![]() ;
;
⑤当![]() 时,有
时,有![]() .
.
其中正确结论的个数是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】
根据抛物线对称轴方程对①进行判断;由抛物线开口方向得到a<0,由对称轴位置可得b>0,由抛物线与y轴的交点位置可得c>0,于是可对②进行判断;根据顶点坐标对③进行判断;根据抛物线的对称性对④进行判断;根据函数图象得当1<x<4时,一次函数图象在抛物线下方,则可对⑤进行判断.
∵抛物线的顶点坐标A(1,3),
∴抛物线的对称轴为直线![]()
∴2a+b=0,所以①正确;
∵抛物线开口向下,
∴a<0,
∴b=2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以②错误;
∵抛物线的顶点坐标A(1,3),
∴x=1时,二次函数有最大值,
∴方程ax2+bx+c=3有两个相等的实数根,所以③正确;
∵抛物线与x轴的一个交点为(4,0)
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(2,0),所以④错误;
∵抛物线y1=ax2+bx+c与直线y2=mx+n(m≠0)交于A(1,3),B点(4,0)
∴当1<x<4时,y2<y1,所以⑤正确。
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度
 米,顶点
米,顶点 距水面
距水面 米(即
米(即 米),小孔顶点
米),小孔顶点 距水面
距水面 米(即
米(即 米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,则此时大孔的水面宽度
米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,则此时大孔的水面宽度 长为( )
长为( )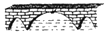

A.
 米 B.
米 B.  C.
C.  米 D.
米 D.  米
米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某二次函数的图象,将其向左平移
 个单位后的图象的函数解析式为
个单位后的图象的函数解析式为 ,则下列结论中正确的有( )
,则下列结论中正确的有( ) ;
; ;
; ;
; .
.
A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形
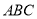 底边
底边 的长为
的长为 ,面积是
,面积是 ,腰
,腰 的垂直平分线
的垂直平分线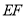 交
交 于点
于点 ,若
,若 为
为 边上的中点,
边上的中点, 为线段
为线段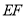 上一动点,则
上一动点,则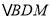 的周长的最小值为( )
的周长的最小值为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个二次函数的图象,三位同学分别说出了它的一些特点:
甲:对称轴为直线x=4
乙:与x轴两个交点的横坐标都是整数.
丙:与y轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)操作发现:如图①,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边在CD上方作等边△CDE,连接AE,则AE与BD有怎样的数量关系?说明理由.
(2)类比猜想:如图②,若点D是等边△ABC的边BA延长线上一动点,连接CD,以CD为边在CD上方作等边△CDE,连接AE,请直接写出AE与BD满足的数量关系,不必说明理由;

相关试题

