【题目】已知关于x的方程x2-3x+c=0有两个实数根.
(1)求c的取值范围;
(2)若c为正整数,取符合条件的c的一个值,并求出此时原方程的根.
参考答案:
【答案】(1)c≤![]() ;(2)当c=2时,x1=1,x2=2;当c=1时,x1=
;(2)当c=2时,x1=1,x2=2;当c=1时,x1=![]() ,x2=
,x2=![]()
【解析】
(1)先根据方程有两个实数根可知△≥0,由△≥0可得到关于c的不等式,求出c的取值范围即可;
(2)由(1)中c的取值范围得出符合条件的c的正整数值,代入原方程,利用因式分解法或求根公式即可求出x的值.
(1)解:∵方程有两个实根,∴△=b2-4ac=9-4c≥0,∴c≤![]() ;
;
(2)解:∵c≤![]() ,且c为正整数,∴c=1或c=2.
,且c为正整数,∴c=1或c=2.
取c=2,方程为x2-3x+2=0,∴(x-1)(x-2)=0
解得:x1=1,x2=2.
也可如下:
取c=1,方程为x2-3x+1=0,解得:x1= ![]() ,x2=
,x2=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=
 (x>0)的图象与矩形OABC的边BC交于点D,分别过点A,D作AF∥DE,交直线y=k2x(k2<0)于点F,E.若OE=OF,BD=2CD,四边形ADEF的面积为12,则k1的值为________.
(x>0)的图象与矩形OABC的边BC交于点D,分别过点A,D作AF∥DE,交直线y=k2x(k2<0)于点F,E.若OE=OF,BD=2CD,四边形ADEF的面积为12,则k1的值为________. 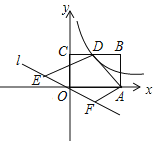
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线
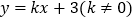 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线 的一个交点为B(-1,4).
的一个交点为B(-1,4).(1)求直线与双曲线的表达式;
(2)过点B作BC⊥x轴于点C,若点P在双曲线
 上,且△PAC的面积为4,求点P的坐标.
上,且△PAC的面积为4,求点P的坐标.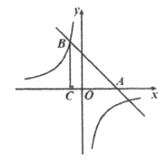
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.

(1)求证:△ABN≌△CDM;
(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小明解方程
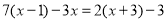 的过程,请你仔细阅读,并解答所提出的问题:
的过程,请你仔细阅读,并解答所提出的问题:解:去括号,得
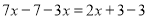 . (第一步)
. (第一步)移项,得
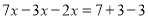 . (第二步)
. (第二步)合并同类项,得
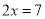 . (第三步)
. (第三步)系数化为1,得
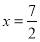 . (第四步)
. (第四步)(1)该同学解答过程从第_____步开始出错,错误原因是______________________;
(2)写出正确的解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产B产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择那种生产方案,使生产这60件产品的成本最低?(成本=材料费+加工费)
-
科目: 来源: 题型:
查看答案和解析>>【题目】两辆汽车从相距84 km的两地同时出发相向而行,甲车的速度比乙车的速度快20 km/h,半小时后两车相遇.
(1)求乙车的速度是每小时多少千米?
(2)甲车的速度是_______ km/h;
(3)两车相遇时,甲车比乙车多行驶________千米.
相关试题

