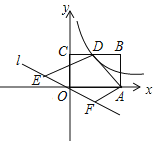
【题目】如图,函数y= ![]() (x>0)的图象与矩形OABC的边BC交于点D,分别过点A,D作AF∥DE,交直线y=k2x(k2<0)于点F,E.若OE=OF,BD=2CD,四边形ADEF的面积为12,则k1的值为________.
(x>0)的图象与矩形OABC的边BC交于点D,分别过点A,D作AF∥DE,交直线y=k2x(k2<0)于点F,E.若OE=OF,BD=2CD,四边形ADEF的面积为12,则k1的值为________.
参考答案:
【答案】4
【解析】
如图,连接OD,过O作OM∥ED交AD于M,可以得出S△AOD=![]() S四边形ADEF,进而得到S矩形OACB的值.作DH⊥OA于H,可得S矩形OCDH,从而得到结论.
S四边形ADEF,进而得到S矩形OACB的值.作DH⊥OA于H,可得S矩形OCDH,从而得到结论.
解:如图,连接OD,过O作OM∥ED交AD于M.
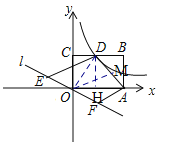
S△AOD=S△AOM+S△DOM=![]() OM×h1+
OM×h1+![]() OM×h2==
OM×h2==![]() OM(h1+h2),S四边形ADEF=
OM(h1+h2),S四边形ADEF=![]() (AF+ED)h.
(AF+ED)h.
又∵OM=![]() (AF+ED),h1+h2=h,故S△AOD=
(AF+ED),h1+h2=h,故S△AOD=![]() S四边形ADEF=
S四边形ADEF=![]() ×12=6.
×12=6.
∵△AOD和矩形OACB同底等高,故S矩形OACB=12,作DH⊥OA于H.
∵ BD=2CD ,BC=3CD,故S矩形OCDH=![]() ×12=4,即CD×DH=xy=k1=4.
×12=4,即CD×DH=xy=k1=4.
故答案为:4.
-
科目: 来源: 题型:
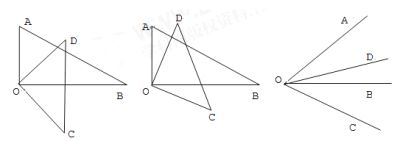
查看答案和解析>>【题目】(1) 将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起, ∠AOB=∠DOC=90°.
①如图(1),若OD是∠AOB的平分线时,求∠BOD和∠AOC的度数.
②如图(2),若OD不是∠AOB的平分线,试猜想∠AOC与∠BOD的数量关系,并说明理由.
(2)如图(3),如果两个角∠AOB = ∠DOC= m°(0< m <90),直接写出∠AOC与∠BOD的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD为正方形,E是BC的中点,连接AE,过点A作∠AFD,使∠AFD=2∠EAB,AF交CD于点F,如图①,易证:AF=CD+CF.
(1)如图②,当四边形ABCD为矩形时,其他条件不变,线段AF,CD,CF之间有怎样的数量关系?请写出你的猜想,并给予证明;
(2)如图③,当四边形ABCD为平行四边形时,其他条件不变,线段AF,CD,CF之间又有怎样的数量关系?请直接写出你的猜想.
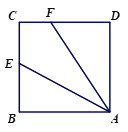
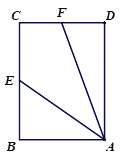
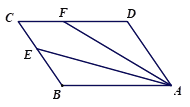
图① 图② 图③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN相交于点P,CN与DQ相交于点M,判断四边形MNPQ的形状,并证明你的结论.
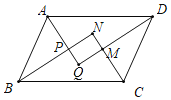
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线
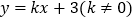 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线 的一个交点为B(-1,4).
的一个交点为B(-1,4).(1)求直线与双曲线的表达式;
(2)过点B作BC⊥x轴于点C,若点P在双曲线
 上,且△PAC的面积为4,求点P的坐标.
上,且△PAC的面积为4,求点P的坐标.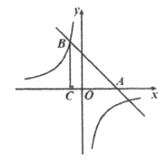
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.

(1)求证:△ABN≌△CDM;
(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2-3x+c=0有两个实数根.
(1)求c的取值范围;
(2)若c为正整数,取符合条件的c的一个值,并求出此时原方程的根.
相关试题

