【题目】关于x的方程x2+(2k+1)x+k2+2=0有两个实数根x1、x2
(1)求实数k的取值范围;
(2)若x1、x2满足|x1|+|x2|=|x1x2|﹣1,求k的值.
参考答案:
【答案】
(1)解:根据题意得△=(2k+1)2﹣4(k2+2)≥0,
解得k≥ ![]()
(2)解:根据题意得x1+x2=﹣(2k+1)<0,x1x2=k2+2>0,
∴x1<0,x2<0,
∵|x1|+|x2|=|x1x2|﹣1,
∴﹣(x1+x2)=x1x2﹣1,
∴2k+1=k2+2﹣1,
整理得k2﹣2k=0,解得k1=0,k2=2,
∵k≥ ![]() ,
,
∴k=2
【解析】(1)根据判别式的意义得到△=(2k+1)2﹣4(k2+2)≥0,然后解不等式即可;(2)根据根与系数的关系得到x1+x2=﹣(2k+1)<0,x1x2=k2+2>0,则利用有理数的乘法性质可判断x1<0,x2<0,然后去绝对值得到﹣(x1+x2)=x1x2﹣1,则2k+1=k2+2﹣1,整理得到k2﹣2k=0,再解关于k的方程即可得到满足条件的k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠BOC=α.
(1)若α=40°,OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数;
(2)若∠AOD=
 ∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;
∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;(3)若∠AOD=
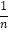 ∠AOC,∠DOE=
∠AOC,∠DOE=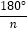 (n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).
(n≥2,且n为正整数),如图(c)所示,请用α和n表示∠AOE的度数(直接写出结果).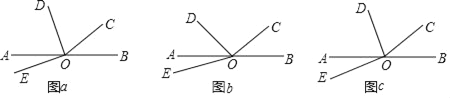
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两点在数轴上的位置如图所示,其中O为原点,点A对应的有理数为﹣4,点B对应的有理数为6.
(1)动点P从点A出发,以每秒2个单位长度的速度向右运动,设运动时间为t秒(t>0).
①当t=1时,AP的长为 ,点P表示的有理数为 ;
②当PB=2时,求t的值;
(2)如果动点P以每秒6个单位长度的速度从O点向右运动,点A和B分别以每秒1个单位长度和每秒3个单位长度的速度向右运动,且三点同时出发,那么经过几秒PA=2PB.

-
科目: 来源: 题型:
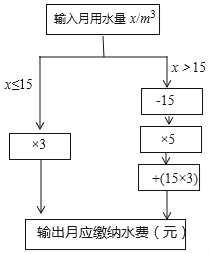
查看答案和解析>>【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户
张大爷
王阿姨
小明家
月用水量/m3
6
15
17
月应缴纳水费/元
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1 cm,△ACD的周长为12 cm,则△ABC的周长是( )

A. 13 cm B. 14 cm C. 15 cm D. 16 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点A,B,C都是格点.
(1)将△ABC向左平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2,请画出△A2B2C2;
(3)作出△ABC关于直线l对称的△A3B3C3,使A,B,C的对称点分别是A3,B3,C3;
(4)△A2B2C2与△A3B3C3成______________△A1B1C1与△A2B2C2成_____________(填“中心对称”或“轴对称”).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.

(1)快艇从港口B到小岛C需要多长时间?
(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.
相关试题

