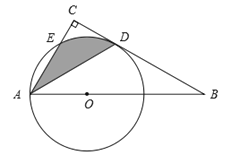
【题目】如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求∠CAD的度数;
(2)若OA = 2,求阴影部分的面积(结果保留π).
【答案】(1)∠CAD的度数为30°;
(2)阴影部分的面积为![]() .
.
【解析】试题分析:(1)连接OD.由切线的性质可知OD⊥BC,从而可证明AC∥OD,由平行线的性质和等腰三角形的性质可证明∠CAD=∠OAD;(2)连接OE,ED、OD.先证明ED∥AO,然后依据同底等高的两个三角形的面积相等可知S△AED=S△EDO,于是将阴影部分的面积可转化为扇形EOD的面积求解即可.
试题解析:(1)连接OD,
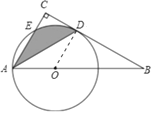
∵BC是⊙O的切线,D为切点,
∴OD⊥BC.
又∵AC⊥BC,
∴OD∥AC,
∴∠ADO=∠CAD.
又∵OD=OA,
∴∠ADO=∠OAD,
∴∠CAD=∠OAD=30°.
(2)连接OE,ED.

∵∠BAC=60°,OE=OA,
∴△OAE为等边三角形,
∴∠AOE=60°,
∴∠ADE=30°.
又∵![]() ,
,
∴∠ADE=∠OAD,
∴ED∥AO,
∴![]()
∴阴影部分的面积 = ![]() .
.
【题型】解答题
【结束】
6
【题目】如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),求这个立体图形的表面积.

参考答案:
【答案】200mm2.
【解析】试题分析:根据三视图可知立体图形下面的长方体的长、宽、高分别为8mm,6mm,2mm,上面的长方体的长、宽、高分别为4mm,2mm,4mm.由此计算这个立体图形的表面积即可.
试题解析:
根据三视图可知立体图形下面的长方体的长、宽、高分别为8mm,6mm,2mm,上面的长方体的长、宽、高分别为4mm,2mm,4mm.
则这个立体图形的表面积为:2(8×6+6×2+8×2)+2(4×2+2×4+4×4)-2×4×2=200(mm2).
答:这个立体图形的表面积为200mm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用了随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.

请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 .
(2)请补全条形统计图.
(3)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用画树状图或列表的方法求出恰好抽到1个男生和1个女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是常见的安全标记,其中是轴对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
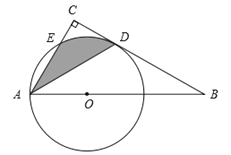
查看答案和解析>>【题目】如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求∠CAD的度数;
(2)若OA = 2,求阴影部分的面积(结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物
 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物
 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.
【答案】(1)5.6m;(2)应挪走.
【解析】试题解析:试题分析:(1)在构建的直角三角形中,首先求出两个直角三角形的公共直角边,进而在Rt△ACD中,求出AC的长.
(2)通过解直角三角形,可求出BD、CD的长,进而可求出BC、PC的长.然后判断PC的值是否大于2米即可.试题解析:(1)如图,
在Rt△ABD中,AD=ABsin45°=4 .
.
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=8.
即新传送带AC的长度约为8米;
(2)结论:货物MNQP不用挪走.
解:在Rt△ABD中,BD=ABcos45°=4 =4.
=4.
在Rt△ACD中,CD= AD=4
AD=4 .
.
∴CB=CD-BD=4 -4≈2.8.
-4≈2.8.
∵PC=PB-CB≈5-2.8=2.2>2,
∴货物MNQP不应挪走.【题型】解答题
【结束】
8【题目】如图有一圆锥形粮堆,其主视图是边长为6m的正三形ABC。
(1)求该圆锥形粮堆的侧面积。
(2)母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,求小猫经过的最短路程。 (结果不取近似数)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xoy中,一次函数
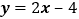 的图象与x轴、y轴分别交于A、B两点,
的图象与x轴、y轴分别交于A、B两点, 为一次函数
为一次函数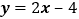 的图象上一点.
的图象上一点. 直接写出A、B两点的坐标:
直接写出A、B两点的坐标: ______,______
______,______ ,
, ______,______
______,______
 若
若 ,求k的取值范围;
,求k的取值范围; 若点Q为一次函数
若点Q为一次函数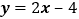 图象上第一象限内一点
图象上第一象限内一点 且满足
且满足 ,
, ,求
,求 的值;
的值; 一次函数
一次函数 的图象与一次函数
的图象与一次函数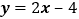 的图象交于C点,与y轴交于点D,直线OP与直线AB、直线CD不能围成三角形,直接写出符合条件的P点的坐标.
的图象交于C点,与y轴交于点D,直线OP与直线AB、直线CD不能围成三角形,直接写出符合条件的P点的坐标.
相关试题

