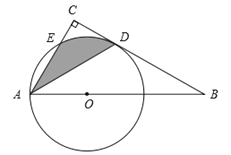
【题目】如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求∠CAD的度数;
(2)若OA = 2,求阴影部分的面积(结果保留π).
参考答案:
【答案】(1)∠CAD的度数为30°;
(2)阴影部分的面积为![]() .
.
【解析】试题分析:(1)连接OD.由切线的性质可知OD⊥BC,从而可证明AC∥OD,由平行线的性质和等腰三角形的性质可证明∠CAD=∠OAD;(2)连接OE,ED、OD.先证明ED∥AO,然后依据同底等高的两个三角形的面积相等可知S△AED=S△EDO,于是将阴影部分的面积可转化为扇形EOD的面积求解即可.
试题解析:(1)连接OD,
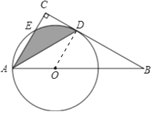
∵BC是⊙O的切线,D为切点,
∴OD⊥BC.
又∵AC⊥BC,
∴OD∥AC,
∴∠ADO=∠CAD.
又∵OD=OA,
∴∠ADO=∠OAD,
∴∠CAD=∠OAD=30°.
(2)连接OE,ED.
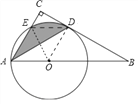
∵∠BAC=60°,OE=OA,
∴△OAE为等边三角形,
∴∠AOE=60°,
∴∠ADE=30°.
又∵![]() ,
,
∴∠ADE=∠OAD,
∴ED∥AO,
∴![]()
∴阴影部分的面积 = ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=BD;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校开展课外体育活动,决定开展:篮球、乒乓球、踢毽子、跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种).随机抽取了部分学生进行调查,并将调查结果绘成如下统计图,请你结合图中信息解答下列问题.
(1)样本中最喜欢篮球项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=(x﹣1)2﹣2的图象可看作由函数y=x2的图象( )
A.先向右平移1个单位长度,再向上平移2个单位长度
B.先向左平移1个单位长度,再向上平移2个单位长度
C.先向左平移1个单位长度,再向下平移2个单位长度
D.先向右平移1个单位长度,再向下平移2个单位长度
-
科目: 来源: 题型:
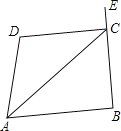
查看答案和解析>>【题目】如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°
(1)∠DCA的度数;
(2)∠DCE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若三角形三边分别为6,8,10,那么它最长边上的中线长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件夹克衫先按成本价提高60%标价,再将标价打7折出售,结果获利36元,设这件夹克衫的成本价是x元,那么根据题意,所列方程正确的是( )
A. 0.7(1+0.6)x=x﹣36B. 0.7(1+0.6)x=x+36
C. 0.7(1+0.6x)=x﹣36D. 0.7(1+0.6x)=x+36
相关试题

